This project is also available on https://www.covid19.victoryap.com/
Table of contents¶
Section A: Explanatory Data Analysis¶
2 Exploratory Data Analysis
3 Cases
= 3.1. Overview of the cases in Korea
== 3.1.1. Column to use
== 3.1.2. Map Visualisation of cases in Korea
= 3.2. Check the relationship between group and solo cases
== 3.2.1. Bar chart visualisation of cases in Korea
== 3.2.2. Calculation of individual & group cases
= 3.3. Source of infected cases sort by source and province
= 3.4. Risk Level of each province
4 Patient Info
= 4.1. Basic Analysis
== 4.1.1. Numbers Of Cases Per Day
== 4.1.2. Does infection have something to do with gender, age, or geographical location?
= 4.2. Average Survivor Treatment Day (Recovery Speed), By Age and Gender
= 4.3. Average Survivor Treatment Day (Recovery Speed) By City & Age
= 4.4. Average Deceased Treatment Day (Fatality Speed) By Gender and Age
= 4.5. Average Deceased Treatment Day (Fatality Speed) By City and Age
= 4.6. Number of Infection, Survivor, Deceased Per City by percentage
= 4.7. Number of Infection, Survivor, Deceased Sort By Gender
= 4.8. Network Diagram
Section B: Time Series Analysis¶
5 Policy & Search Trend
6 Time
= 6.1. Test & Negative cases daily average increase amount by day
= 6.2. Test & Negative cases daily average increase amount by month
= 6.3. Confirmed, released & deceased cases daily average increase amount by day
= 6.4. Confirmed, released & deceased cases daily average increase amount by month
= 6.5. Temporal Distribution and Prediction
= 6.6. Stationarity Testing
= 6.7. Seasonal Decomposition
= 6.8. ARIMA Modelling
= 6.9. ETS Modelling
= 6.10.Facebook Prophet
7 Time Age
= 7.1. Deceased vs confirmed cases across different age group over time
= 7.2. Testing of Homogeneous Mortality Hypothesis
= 7.3. Does TimeAge Dataset tallies with the patient.csv ?
= 7.4. Deceased Rate
8 Time Gender
= 8.1. Deceased vs confirmed cases across different gender over time
= 8.2. Confirmed cases daily average increase amount by month (Sort by gender)
= 8.3. Confirmed cases daily average increase amount by day (Sort by gender)
= 8.4. Deceased cases daily average increase amount by month (Sort by gender)
= 8.5. Deceased cases daily average increase amount by day (Sort by gender)
= 8.6. Mortality Rates across Gender Groups
9 Time Province
= 9.1. Deceased vs confirmed cases across different province over time (With Daegu)
= 9.2. Deceased vs confirmed cases across different province over time (Without Daegu)
= 9.3. Mortality Rates across Provinces
= 9.4. Does TimeProvince Dataset tallies with the cases.csv & patient.csv?
10 In depth Analysis Of Daegu Cases using Technical Analysis
= 10.1 Technical Analysis
= 10.2 Stats By Month
= 10.3 Stats By Day
11 Time Series World Map Visualisation of COVID-19 cases in korea
= 11.1 With Animation
= 11.2 Without animation
12 Weather
= 12.1 Busan Avg Temp (Mean) vs Most Wind Direction (Mean) Analysis for days with wind direction greater than 100
= 12.2 Does other region has the same relationship between avg_temp and most_wind direction?
13 Region
= 13.1 Number of nusing home and elder population ratio across Korea
= 13.2 Correlation between elder population ratio and number of cases
Section C: Web Scalping¶
14 Web Scalping: Comparsion across the world
= 14.1 Getting the data from the table
= 14.2 Covert to data
= 14.3 Worldwide Total Cases Chart
= 14.4 Worldwide Total Death Chart
= 14.5 Scatterplot between total cases and total death
Section D: Summary from EDA¶
15 Summarise Key findings from Exploratory Data Analysis
= 15.1 Overall Cases in Korea
= 15.2 Patient Cases
= 15.3 Policy
= 15.4 Cases Over Time Analysis
= 15.5 Cases Over Age & Time Analysis
= 15.6 Cases Over Gender & Time Analysis
= 15.7 Cases Over Province & Time Analysis
= 15.8 Weather
= 15.9 Number of nursing home vs Population Ratio
Section E: Predictive modelling¶
16 Preparing the data for modelling
= 16.1 Get the necessary columns
= 16.2 Calculate number of days of treatment before dropped date column
= 16.3 Convert state, gender and gender columns to categorical data
= 16.4 Get dummy for province
17 Correlation Matrix
18 Building Machine Learning Models Part 1
= 18.1 Stochastic Gradient Descent (SGD)
= 18.2 Random Forest
= 18.3 Logistic Regression
= 18.4 Gaussian Naive Bayes
= 18.5 K Nearest Neighbor
= 18.6 Perceptron
= 18.7 Linear Support Vector Machine
= 18.8 Decision Tree
= 18.9 Getting the best model
= 18.10 Decision Tree Diagram
= 18.11 What is the most important feature ?
= 18.12 Confusion Matrix with Precision & Recall & F-Score
19 Building Machine Learning Models Part 2
= 19.1 Random Forest
= 19.2 Decision Tree
= 19.3 Getting the best model
= 19.4 Decision Tree Diagram
= 19.5 Importance
= 19.6 Confusion Matrix with Precision & Recall & F-Score
20 Refine Dataset for Machine Learning
= 20.1 Preparing the data for modelling
= 20.2 Building Machine Learning Models Part 3
= 20.3 Importances
= 20.4 Confusion Matrix with Precision & Recall & F-Score
= 20.5 Summary
Section F: Final Summary¶
21 Step to take to control the COVID-19 situation even better
= 21.1 Abraham Wald and the Missing Bullet Holes
= 21.2 Survivorship Bias
= 21.3 Improving the situation
22 References
23 Appendix
24 Contribution Statements
%%javascript
IPython.OutputArea.prototype._should_scroll = function(lines) {
return false;
}
import pandas as pd
import numpy as np
import seaborn as sns
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
import networkx as nx
import plotly
from plotly.offline import download_plotlyjs, init_notebook_mode, iplot
import plotly.graph_objs as go
import plotly.figure_factory as ff
import plotly.express as px
px.set_mapbox_access_token(open("./mapbox_token").read())
from plotly.subplots import make_subplots
from matplotlib import gridspec
from bs4 import BeautifulSoup
from warnings import filterwarnings
filterwarnings('ignore')
from datetime import datetime
import requests
# Algorithms
from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.naive_bayes import GaussianNB
# Matrix
from sklearn.metrics import precision_score, recall_score
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
from sklearn.metrics import f1_score
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
from sklearn.metrics import precision_recall_curve
# Diagram
from sklearn.tree import export_graphviz
import pydotplus
from sklearn.externals.six import StringIO
from IPython.display import Image
from keras.models import Sequential
from keras.layers import LSTM, Dense
from dateutil.easter import easter
from fbprophet import Prophet
from statsmodels.tsa.holtwinters import ExponentialSmoothing, Holt
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import adfuller, kpss
import pmdarima as pm
import scipy.stats as scs
2) Exploratory Data Analysis ¶
3) Case ¶
3.1) Overview of the cases in Korea ¶
3.1.1) Column to use ¶
case = pd.read_csv("covid/Case.csv")
case.groupby("city")["confirmed"].sum().sort_values(ascending = False)
case.groupby("city")["confirmed"].sum().sort_values(ascending = False).iloc[1:3]/case["confirmed"].sum() * 100
Since city has around 42% confirmed cases that is not classified, we shall use province
3.1.2) Map Visualisation of cases in Korea ¶
caseData = pd.read_csv('covid/case.csv')
caseDataForMap = caseData.copy()
caseDataForMap = caseDataForMap[caseDataForMap[['latitude', 'longitude']] != '-']
cols = ['latitude', 'longitude']
caseData[cols] = caseData[cols].apply(pd.to_numeric, errors='coerce', axis=1)
display(caseData.head())
fig = px.scatter_mapbox(
caseData[caseData.latitude != '-'],
text="<br>City: " + caseData["city"] +" <br>Province: " + caseData["province"],
lat="latitude",
lon="longitude",
color="confirmed",
size="confirmed",
color_continuous_scale=px.colors.sequential.Burg,
size_max=100,
mapbox_style='dark',
zoom=6,
title="Overview of the cases in Korea")
fig.show()
Majority of the cases is concentrated in Daegu while the rest of the areas have lower amount of cases.
It seems there are 2 huge cluster in Korea regarding Covid-19 cases. One of the cluster is in the province of Daegu.
And another cluster is in the province of seoul
3.2) Check the relationship between group and solo cases ¶
3.2.1) Bar chart visualisation of cases in Korea ¶
caseData = pd.read_csv('covid/case.csv')
caseDataForMap = caseData.copy()
caseDataSorted = caseDataForMap.sort_values(by=['confirmed'], ascending=False)
display(caseDataSorted.head())
sortedValues = caseDataForMap.groupby(['province','group']).sum().sort_values(by=['confirmed'], ascending=False).reset_index()
sortedValues = sortedValues[['province','confirmed','group']]
display(sortedValues.head())
fig = px.bar(sortedValues, x='confirmed', y='province', color='group', barmode='group')
fig.update_layout(hovermode='y')
fig.show()
In general, there are more group cases than non-group cases in korea.
The only prominent exception is Busan.
This may imply that people are more prone to covid-19 when they are in group
3.2.2) Calculation of individual & group cases¶
case_pivot = case.pivot_table(values = "confirmed",index = "province",columns = "group", aggfunc = "sum")
case_pivot = pd.DataFrame(case_pivot.to_records())
case_pivot.rename(columns = {"False": "Group_False","True": "Group_True"}, inplace = True)
case_pivot.set_index("province", inplace = True)
print("There are a total of {} individual cases".format(case_pivot["Group_False"].sum()))
print("There are a total of {} group cases".format(case_pivot["Group_True"].sum()))
Where are the reported cases located? Are they in group or individual reports?¶
The majority of the reported cases are located in Daegu province. The virus spreads easily in a group setting.
3.3) Source of infected cases sort by source and province ¶
locations = caseData.pivot("province", "infection_case", "confirmed")
display(locations.head())
f, ax = plt.subplots(figsize=(20, 5))
sns.heatmap(locations, cmap="gnuplot", annot=False, fmt="d", linewidths=.5, ax=ax).set_title('Numbers of cases sort by source and province')
fig = px.sunburst(caseDataSorted,
path=['province', 'infection_case'],
values='confirmed',
width=1000, height=600)
fig.show()
The top covid sources for
- Daegu is Shincheonji church
- Gyeongsangbuk-do is Shincheonji church
- Seoul is overseas inflow
- Gyeonggi-do is overseas inflow
- Incheon is overseas inflow
fig = px.sunburst(caseDataSorted,
path=['infection_case', 'province'],
values='confirmed',
width=1000, height=600)
fig.show()
The top 5 sources for covid-19 comes from
- Shincheonji Church
- Contract With patient
- Unknown Sources
- Overseas inflow
- Itaewon clubs
3.4) Risk Level of each province ¶
caseData = pd.read_csv('covid/case.csv')
caseDataForMap = caseData.copy()
caseDataForMap['logConfirmed'] = np.log(caseDataForMap['confirmed'])
display(caseDataForMap.head())
fig = px.box(caseDataForMap, x="logConfirmed", y="province")
fig.update_traces(quartilemethod="exclusive") # or "inclusive", or "linear" by default
fig.update_layout(hovermode='y')
fig.show()
caseDataForMap = caseData.copy()
sortedValues = caseDataForMap.groupby(['province']).sum().sort_values(by=['confirmed'], ascending=False).reset_index()
sortedValues['logConfirmed'] = np.log(sortedValues['confirmed'])
sortedValues = sortedValues[['province','confirmed','logConfirmed']]
display(sortedValues.head())
print('Mean: ', sortedValues.mean().values)
print('Standard Derivation: ', sortedValues.std().values)
This amount of COVID-19 cases has a mean of 670 and a standard deviation of 1610.
Hence we sort the provinces into 4 different types of level:
- Very Risk = 4 (Above 2000 cases)
- High Risk = 3 (1000 - 2000 cases)
- Medium Risk = 2 (100 - 999 cases)
- Low Risk = 1 ( Below 99 cases)
def calculate_risk_level(sortedValues) :
if sortedValues['confirmed'] >= 2000:
return 4
elif sortedValues['confirmed'] >= 1000 and sortedValues['confirmed'] < 2000:
return 3
elif sortedValues['confirmed'] >= 100 and sortedValues['confirmed'] < 900:
return 2
else:
return 1
sortedValues['Risk Level'] = sortedValues.apply(calculate_risk_level,axis=1);
sortedValues = sortedValues[['province','Risk Level']]
display(sortedValues.head())
4) Patient Info ¶
4.1) Data Analysis ¶
4.1.1) Numbers Of Cases Per Day ¶
patientData = pd.read_csv('covid/patientinfo.csv')
display(patientData.head())
groupPatientData = patientData.groupby('confirmed_date').size().reset_index()
groupPatientData.columns = ['confirmed_date', 'count']
fig = px.line(groupPatientData, x="confirmed_date", y="count", title='Numbers Of Covid Cases Per Day')
fig.update_layout(hovermode='x')
fig.show()
The covid cases has a spike from Feb-Mar period before it gradually reduces from Mar-May period.
During June, the covid cases had a minor rebound.
4.1.2) Does infection have something to do with gender, age, or geographical location? ¶
patient = pd.read_csv("covid/PatientInfo.csv")
patient.head()
patient.isna().sum()
Since we're looking for gender, age and geograhical location, dropping those NaN data for the age group would suffice as it has the highest NaN among these parameters.
patient.dropna(subset = ["age"], inplace = True)
patient.isna().sum()
patient.patient_id.count()
We have 3,782 patient info as opposed to 11,395 reported cases in case.csv. Patient info is a small subset of the total number of cases. Let's look into the dataset
pct_gender = patient.groupby("sex")["patient_id"].count()/patient["patient_id"].count()
pct_gender
def plot_bar(df, palette = None):
fig, ax = plt.subplots(figsize = (8,5))
sns.barplot(x = df.index, y = df, palette = palette)
ax.tick_params(axis = "both", labelsize = 15)
plot_bar(pct_gender, "Paired")
plt.xlabel("Gender", size = 15)
plt.ylabel("Confirmed Cases in %", size = 15)
plt.title("Confirmed Cases by Gender", size = 15)
plt.show()
Gender seems to be even
patient_age = patient.groupby("age")["patient_id"].count().drop(index = "100s").sort_index()
patient_age
plot_bar(patient_age)
plt.xlabel("Age", size = 15)
plt.ylabel("Number of patients", size = 15)
plt.title("Age Group of Patient", size = 15)
plt.show()
There are many confirmed cases in the 20s age group. This could be probably that they have more social activities like attending university, hanging out with friends and dating.
patient_province = patient.groupby("province")["patient_id"].count()
plot_bar(patient_province, "rocket")
plt.xlabel("Age", size = 15)
plt.ylabel("Number of patients", size = 15)
plt.title("Province of confirmed cases", size = 15)
plt.xticks(rotation = 90)
plt.show()
Patient.csv Data is not a representative of the overall Dataset as Daegu does not have the highest confirmed cases when we compare it to the cases.csv
4.2) Average Survivor Treatment Day (Recovery Speed), By Age and Gender ¶
confinedDaysAnalysis = patientData.copy()
confinedDaysAnalysis = confinedDaysAnalysis[confinedDaysAnalysis['age'] != '100s'] #Just a single data which is highly skewed
confinedDaysAnalysis = confinedDaysAnalysis[confinedDaysAnalysis['released_date'].notnull()]
cols = ['released_date', 'confirmed_date']
confinedDaysAnalysis[cols] = confinedDaysAnalysis[cols].apply(pd.to_datetime, errors='coerce', axis=1)
confinedDaysAnalysis['Total Treatment Days'] = (confinedDaysAnalysis['released_date'] - confinedDaysAnalysis['confirmed_date']).dt.days
groupedData = confinedDaysAnalysis.groupby(['sex', 'age'])['Total Treatment Days'].mean().unstack().stack().reset_index()
groupedData.columns = ["sex", "age", "Average Treatment Days"]
dataForHeatmap = groupedData.pivot("sex", "age", "Average Treatment Days")
display(dataForHeatmap.head())
f, ax = plt.subplots(figsize=(15, 5))
sns.heatmap(dataForHeatmap, cmap="RdPu", annot=False, fmt="d", linewidths=.5, ax=ax).set_title('Average Survivor Treatment Day, Sort by Age & Gender')
In general, the older the patient, the longer it will take for them to recover
confinedDaysAnalysis['age'] = confinedDaysAnalysis['age'].dropna()
age = {'0s':0, '10s':1, '20s':2, '30s':3, '40s':4, '50s':5, '60s':6, '70s':7, '80s':8, '90s':9}
confinedDaysAnalysis['age'] = confinedDaysAnalysis['age'].map(age)
confinedDaysAnalysis = confinedDaysAnalysis[confinedDaysAnalysis['age'].notna()]
fig = px.scatter(confinedDaysAnalysis, x="age", y="Total Treatment Days", color="sex", trendline="ols", title="Does age group affect total treatment days?")
fig.update_layout(hovermode='y')
fig.show()
With a R squared value of 0.03, it seems that the age of the patient has little effect on the number of days it take for them to recover from covid-19
4.3) Average Survivor Treatment Day (Recovery Speed) By City & Age ¶
groupedData = confinedDaysAnalysis.groupby(['province', 'age'])['Total Treatment Days'].mean().unstack().stack().reset_index()
groupedData.columns = ["province", "age", "Average Treatment Days"]
groupedData['Average Treatment Days'] = np.ceil(groupedData['Average Treatment Days'].apply(pd.to_numeric, errors='coerce'))
dataForHeatmap = groupedData.pivot("province", "age", "Average Treatment Days")
display(dataForHeatmap.head())
f, ax = plt.subplots(figsize=(20, 5))
sns.heatmap(dataForHeatmap, cmap="RdPu", annot=False, fmt="d", linewidths=.5, ax=ax).set_title('Average Survivor Treatment Day, Sort by City & Age')
4.4) Average Deceased Treatment Day (Fatality Speed) By Gender and Age ¶
confinedDaysAnalysis = patientData.copy()
confinedDaysAnalysis = confinedDaysAnalysis[confinedDaysAnalysis['age'] != '100s'] #Just a single data which is highly skewed
confinedDaysAnalysis = confinedDaysAnalysis[confinedDaysAnalysis['deceased_date'].notnull()]
cols = ['deceased_date', 'confirmed_date']
confinedDaysAnalysis[cols] = confinedDaysAnalysis[cols].apply(pd.to_datetime, errors='coerce', axis=1)
confinedDaysAnalysis['Total Treatment Days'] = (confinedDaysAnalysis['deceased_date'] - confinedDaysAnalysis['confirmed_date']).dt.days
display(confinedDaysAnalysis.head())
groupedData = confinedDaysAnalysis.groupby(['sex', 'age'])['Total Treatment Days'].mean().unstack().stack().reset_index()
groupedData.columns = ["sex", "age", "Average Treatment Days"]
dataForHeatmap = groupedData.pivot("sex", "age", "Average Treatment Days")
display(dataForHeatmap.head())
f, ax = plt.subplots(figsize=(15, 5))
sns.heatmap(dataForHeatmap, cmap="RdPu", annot=False, fmt="d", linewidths=.5, ax=ax).set_title('Average Deceased Treatment Day, Sort by Age & Gender')
4.5) Average Deceased Treatment Day (Fatality Speed) By City and Age ¶
groupedData = confinedDaysAnalysis.groupby(['province', 'age'])['Total Treatment Days'].mean().unstack().stack().reset_index()
groupedData.columns = ["province", "age", "Average Treatment Days"]
groupedData['Average Treatment Days'] = np.ceil(groupedData['Average Treatment Days'].apply(pd.to_numeric, errors='coerce'))
dataForHeatmap = groupedData.pivot("province", "age", "Average Treatment Days")
display(dataForHeatmap.head())
f, ax = plt.subplots(figsize=(20, 5))
sns.heatmap(dataForHeatmap, cmap="RdPu", annot=False, fmt="d", linewidths=.5, ax=ax).set_title('Average Deceased Treatment Day, Sort by City & Age')
4.6) Number of Infection, Survivor, Deceased Per City by percentage ¶
survivorCountAnalysis = patientData.copy()
survivorCountAnalysis['survive'] = survivorCountAnalysis['released_date'].notnull()
survivorCountAnalysis['deceased'] = survivorCountAnalysis['deceased_date'].notnull()
survivorCountAnalysis['under treatment'] = survivorCountAnalysis['deceased_date'].isnull() & survivorCountAnalysis['released_date'].isnull()
provinceStats = survivorCountAnalysis.groupby(['province']).sum()
provinceStatsClean = provinceStats[['survive', 'deceased', 'under treatment']]
provinceStatsClean['survive %'] = np.round(provinceStatsClean['survive'] / (provinceStatsClean['survive'] + provinceStatsClean['deceased'] + provinceStatsClean['under treatment']) * 100, 2)
provinceStatsClean['deceased %'] = np.round(provinceStatsClean['deceased'] / (provinceStatsClean['survive'] + provinceStatsClean['deceased'] + provinceStatsClean['under treatment']) * 100, 2)
provinceStatsClean['under treatment %'] = np.round(provinceStatsClean['under treatment'] / (provinceStatsClean['survive'] + provinceStatsClean['deceased'] + provinceStatsClean['under treatment']) * 100, 2)
provinceStatsAbsolute = provinceStatsClean[['survive', 'deceased', 'under treatment']]
provinceStatsPercentage = provinceStatsClean[['survive %', 'deceased %', 'under treatment %']]
display(provinceStatsAbsolute.head())
display(provinceStatsPercentage.head())
newTable = provinceStatsPercentage.reset_index()
display(newTable.head())
newTable = pd.melt(newTable, id_vars="province", var_name="stats", value_name="rate")
display(newTable.head())
fig = px.bar(newTable, x='rate', y='province', color='stats', barmode='group')
fig.update_layout(hovermode='y')
fig.show()
4.7) Number of Infection, Survivor, Deceased Sort By Gender ¶
survivorCountAnalysis = patientData.copy()
survivorCountAnalysis['survive'] = survivorCountAnalysis['released_date'].notnull()
survivorCountAnalysis['deceased'] = survivorCountAnalysis['deceased_date'].notnull()
survivorCountAnalysis['under treatment'] = survivorCountAnalysis['deceased_date'].isnull() & survivorCountAnalysis['released_date'].isnull()
provinceStats = survivorCountAnalysis.groupby(['sex']).sum()
provinceStatsClean = provinceStats[['survive', 'deceased', 'under treatment']]
provinceStatsClean['survive %'] = np.round(provinceStatsClean['survive'] / (provinceStatsClean['survive'] + provinceStatsClean['deceased'] + provinceStatsClean['under treatment']) * 100, 2)
provinceStatsClean['deceased %'] = np.round(provinceStatsClean['deceased'] / (provinceStatsClean['survive'] + provinceStatsClean['deceased'] + provinceStatsClean['under treatment']) * 100, 2)
provinceStatsClean['under treatment %'] = np.round(provinceStatsClean['under treatment'] / (provinceStatsClean['survive'] + provinceStatsClean['deceased'] + provinceStatsClean['under treatment']) * 100, 2)
provinceStatsAbsolute = provinceStatsClean[['survive', 'deceased', 'under treatment']]
provinceStatsPercentage = provinceStatsClean[['survive %', 'deceased %', 'under treatment %']]
display(provinceStatsAbsolute)
display(provinceStatsPercentage)
newTable = provinceStatsPercentage.reset_index()
newTable = pd.melt(newTable, id_vars="sex", var_name="stats", value_name="rate")
display(newTable.head())
fig = px.bar(newTable, x='rate', y='sex', color='stats', barmode='group')
fig.update_layout(hovermode='y')
fig.show()
4.8) Network Diagram ¶
networkData = patientData.copy()
networkData = networkData[networkData['infected_by'].notnull()]
networkData = networkData[['patient_id','sex','age','province','city','infection_case','infected_by','state']]
display(networkData.head())
A = list(networkData["infected_by"].unique())
B = list(networkData["patient_id"].unique())
node_list = set(A+B)
# Create Graph
G = nx.Graph()
for i in node_list:
G.add_node(i)
# G.nodes()
for i,j in networkData.iterrows():
G.add_edges_from([(j["infected_by"],j["patient_id"])])
pos = nx.spring_layout(G, k=0.5, iterations=50)
for n, p in pos.items():
G.nodes[n]['pos'] = p
edge_trace = go.Scatter(
x=[],
y=[],
line=dict(width=0.5,color='#888'),
hoverinfo='none',
mode='lines')
for edge in G.edges():
x0, y0 = G.nodes[edge[0]]['pos']
x1, y1 = G.nodes[edge[1]]['pos']
edge_trace['x'] += tuple([x0, x1, None])
edge_trace['y'] += tuple([y0, y1, None])
node_trace = go.Scatter(
x=[],
y=[],
text=[],
mode='markers',
hoverinfo='text',
marker=dict(
showscale=True,
colorscale='RdPu_r',
reversescale=True,
color=[],
size=15,
colorbar=dict(
thickness=10,
title='Numnber of Infected Cases',
xanchor='left',
titleside='right'
),
line=dict(width=0)))
for node in G.nodes():
x, y = G.nodes[node]['pos']
node_trace['x'] += tuple([x])
node_trace['y'] += tuple([y])
for node, adjacencies in enumerate(G.adjacency()):
node_trace['marker']['color']+=tuple([len(adjacencies[1])])
node_info = str(adjacencies[0]) +' # of connections: '+ str(len(adjacencies[1]))
node_trace['text']+=tuple([node_info])
fig = go.Figure(data=[edge_trace, node_trace],
layout=go.Layout(
title='<br>Korea Covid Network Connections',
titlefont=dict(size=16),
showlegend=False,
hovermode='closest',
margin=dict(b=20,l=5,r=5,t=40),
annotations=[ dict(
text="",
showarrow=False,
xref="paper", yref="paper") ],
xaxis=dict(showgrid=False, zeroline=False, showticklabels=False),
yaxis=dict(showgrid=False, zeroline=False, showticklabels=False)))
iplot(fig)
fig = px.sunburst(networkData, path=['province','infected_by'])
fig.show()
networkData = patientData.copy()
networkData = networkData[networkData['infected_by'].notnull()]
networkData = networkData[['sex','age','province','state','infection_case']]
# print('With NA values')
# display(networkData.count())
# fig = px.parallel_categories(networkData, color_continuous_scale=px.colors.sequential.Inferno)
# fig.show()
# print('Without NA values')
networkData = networkData.dropna()
display(networkData.count())
fig = px.parallel_categories(networkData, color_continuous_scale=px.colors.sequential.Inferno)
fig.show()
5) Policy & Search Trend ¶
searchData = pd.read_csv('covid/searchtrend.csv')
searchDataCopy = searchData.copy()
searchDataMelted = pd.melt(searchDataCopy,
id_vars=['date'],
value_vars=['cold', 'flu','pneumonia','coronavirus'])
searchDataMelted = searchDataMelted[pd.to_datetime(searchDataMelted['date']).dt.year > 2019]
display(searchDataMelted.head())
policyData = pd.read_csv('covid/policy.csv')
policyDataCopy = policyData.copy()
policyDataCopy['end_date'] = policyDataCopy['end_date'].fillna(datetime.now().strftime('%Y-%m-%d'))
display(policyDataCopy.head())
df = []
for index, row in policyDataCopy.iterrows():
df.append(dict(Task=row['gov_policy'], Start=row['start_date'], Finish=row['end_date'], Resource=row['type']))
fig = px.timeline(df, x_start="Start", x_end="Finish", y="Task", color="Resource", title="Policy over time")
fig.update_layout(hovermode='x')
fig.show()
patientData = pd.read_csv('covid/patientinfo.csv')
groupPatientData = patientData.groupby('confirmed_date').size().reset_index()
groupPatientData.columns = ['confirmed_date', 'count']
fig = px.line(searchDataMelted, x="date", y="value", color="variable", title='Search Trend over Time')
fig.update_layout(hovermode='x')
fig.show()
fig = px.line(groupPatientData, x="confirmed_date", y="count", title='Numbers Of Covid Cases Per Day')
fig.update_layout(hovermode='x')
fig.show()
6) Time ¶
timeData = pd.read_csv('covid/time.csv')
timeDataMelted = pd.melt(timeData, id_vars=['date'], value_vars=['test', 'negative','confirmed','released','deceased'])
display(timeDataMelted.head())
fig = px.line(timeDataMelted, x="date", y="value", color='variable', title="Overall cases over time")
fig.update_layout(hovermode='x')
fig.show()
timeDataMelted = pd.melt(timeData, id_vars=['date'], value_vars=['confirmed','released','deceased'])
display(timeDataMelted.head())
fig = px.line(timeDataMelted, x="date", y="value", color='variable', title="Confirmed, released & deceased over time")
fig.update_layout(hovermode='x')
fig.show()
miniTimeData = timeData[['date','test','negative']]
miniTimeData['Test increase'] = miniTimeData['test'] - miniTimeData['test'].shift(1)
miniTimeData['Negative increase'] = miniTimeData['negative'] - miniTimeData['negative'].shift(1)
miniTimeData['Month'] = pd.to_datetime(miniTimeData['date']).dt.month
miniTimeData['Day'] = pd.to_datetime(miniTimeData['date']).dt.day_name()
display(miniTimeData.head())
6.1) Test & Negative cases daily average increase amount by day ¶
miniTimeDataDay = miniTimeData[['Test increase', 'Negative increase', 'Day']]
miniTimeDataDay = miniTimeDataDay.groupby('Day')['Test increase', 'Negative increase'].mean()
cats = [ 'Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday']
miniTimeDataDay = miniTimeDataDay.reindex(cats)
miniTimeDataDay = miniTimeDataDay.reset_index()
miniTimeDataDayMelted = pd.melt(miniTimeDataDay, id_vars=['Day'], value_vars=['Test increase','Negative increase'])
display(miniTimeDataDayMelted.head())
fig = px.bar(miniTimeDataDayMelted, x='Day', y='value', color='variable', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
In general, there are more test conducted during the weekdays
and the number of test conducted is lesser during the weekday
The result might take one day to process which causes a lag in the result of the test cases
6.2) Test & Negative cases daily average increase amount by month ¶
miniTimeDataMonth = miniTimeData[['Test increase', 'Negative increase', 'Month']]
miniTimeDataMonth = miniTimeDataMonth.groupby('Month')['Test increase', 'Negative increase'].mean()
miniTimeDataMonth = miniTimeDataMonth.reset_index()
miniTimeDataMonthMelted = pd.melt(miniTimeDataMonth, id_vars=['Month'], value_vars=['Test increase','Negative increase'])
display(miniTimeDataMonthMelted.head())
fig = px.bar(miniTimeDataMonthMelted, x='Month', y='value', color='variable', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
There are more test conducted during March and June.
This trend also correspond to the the number of covid-19 cases in Korea
It seems that there is a spiked in test conducted whether there is an increase in covid-19 cases
miniTimeData = timeData[['date','confirmed','released','deceased']]
miniTimeData['confirmed increase'] = miniTimeData['confirmed'] - miniTimeData['confirmed'].shift(1)
miniTimeData['released increase'] = miniTimeData['released'] - miniTimeData['released'].shift(1)
miniTimeData['deceased increase'] = miniTimeData['deceased'] - miniTimeData['deceased'].shift(1)
miniTimeData['Month'] = pd.to_datetime(miniTimeData['date']).dt.month
miniTimeData['Day'] = pd.to_datetime(miniTimeData['date']).dt.day_name()
display(miniTimeData.head())
6.3) Confirmed, released & deceased cases daily average increase amount by day ¶
miniTimeDataDay = miniTimeData[['confirmed increase', 'released increase','deceased increase', 'Day']]
miniTimeDataDay = miniTimeDataDay.groupby('Day')['confirmed increase', 'released increase','deceased increase'].mean()
cats = [ 'Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday']
miniTimeDataDay = miniTimeDataDay.reindex(cats)
miniTimeDataDay = miniTimeDataDay.reset_index()
miniTimeDataDayMelted = pd.melt(miniTimeDataDay, id_vars=['Day'], value_vars=['confirmed increase', 'released increase','deceased increase'])
display(miniTimeDataDayMelted.head())
fig = px.bar(miniTimeDataDayMelted, x='Day', y='value', color='variable', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
6.4) Confirmed, released & deceased cases daily average increase amount by month ¶
miniTimeDataMonth = miniTimeData[['confirmed increase', 'released increase','deceased increase', 'Month']]
miniTimeDataMonth = miniTimeDataMonth.groupby('Month')['confirmed increase', 'released increase','deceased increase'].mean()
miniTimeDataMonth = miniTimeDataMonth.reset_index()
miniTimeDataMonthMelted = pd.melt(miniTimeDataMonth, id_vars=['Month'], value_vars=['confirmed increase', 'released increase','deceased increase'])
display(miniTimeDataMonthMelted.head())
fig = px.bar(miniTimeDataMonthMelted, x='Month', y='value', color='variable', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
6.5) Temporal Distribution and Prediction ¶
Visualisation and Description¶
times = pd.read_csv("covid/time.csv")
policies = pd.read_csv("covid/policy.csv")
weathers = pd.read_csv("covid/weather.csv")
times.info()
# Add the datetime index
times["date"] = pd.to_datetime(times.date, format="%Y-%m-%d")
times.set_index("date", inplace=True)
times.head()
fig = plt.figure(figsize=(16, 9))
gs = gridspec.GridSpec(2, 1, height_ratios=[3, 1])
fig.suptitle("Cumulative Reported Cases", size=18)
ax1 = plt.subplot(gs[0])
ax2 = plt.subplot(gs[1], sharex=ax1)
times[["test", "negative"]].plot(ax=ax1, figsize=(16, 9))
times[["confirmed", "released", "deceased"]].plot(ax=ax2, figsize=(16, 9))
plt.tight_layout()
plt.show()
# Create additional variables and plot the positive rate
data = times[["test", "confirmed"]].diff(1)
data["positive_rate"] = data["confirmed"] / data["test"]
fig = plt.figure(figsize=(16, 9))
gs = gridspec.GridSpec(2, 1, height_ratios=[3, 1])
plt.title("Cumulative Reported Cases", size=18)
ax1 = plt.subplot(gs[0])
ax2 = plt.subplot(gs[1], sharex=ax1)
data[["test", "confirmed"]].plot(ax=ax1)
data["positive_rate"].plot(ax=ax2)
ax1.set_title("New Tested and Confirmed Cases", size=18)
ax2.set_title("Positive Rate", size=18)
plt.tight_layout()
plt.show()
# Check the distribution of confirmed cases and positive rates
data["confirmed"].value_counts()
data["confirmed"].plot(kind="hist", figsize=(16, 9))
plt.title("Distribution of Confirmed Cases", size=18)
data["confirmed"].apply(lambda x: x**0.5).plot(kind="hist", figsize=(16, 9))
plt.title("Distribution of Root Confirmed Cases")
data["confirmed"].apply(lambda x: np.log(x) if x!=0 else 0).plot(kind="hist", figsize=(16, 9))
plt.title("Distribution of Log Confirmed Cases", size=18)
# Overall positive rate
times.iloc[-1]["confirmed"] / times.iloc[-1]["test"]
data["positive_rate"].plot(kind="hist", bins=30, figsize=(16, 9))
plt.axvline(x=data["positive_rate"].mean(), color="red")
plt.annotate("x = {:.4f}".format(data["positive_rate"].mean()), xy=(0.02, 50), size=14, color="red")
plt.title("Distribution of Positive Rate", size=18)
# Check how many zeros there are for positive rate
(data["positive_rate"] == 0.0).sum() # Even exclude these cases, there are still many small positive values
data["positive_rate"].plot(kind="line", figsize=(16, 9))
plt.title("Line Graph of Positive Rate", size=18)
As there are too few confirmed cases every day, we will use 5-day and 10-day SMA to show the pattern of positive rate.
# Get the smooth positive rate
fig, ax = plt.subplots(1, 1)
(data["confirmed"].rolling(5).mean() / data["test"].rolling(5).mean()).plot(ax=ax, kind="line", linewidth=2, label="SMA(5)", figsize=(16, 9))
(data["confirmed"].rolling(10).mean() / data["test"].rolling(10).mean()).plot(ax=ax, kind="line", color="darkblue", linewidth=2, label="SMA(10)", figsize=(16, 9))
data["positive_rate"].plot(ax=ax, kind="line", color="magenta", linewidth=2, label="Today", figsize=(16, 9))
plt.legend()
plt.tight_layout()
plt.title("5D and 10D Average Positive Rate", size=18)
# Get the smooth positive rate
fig, ax = plt.subplots(1, 1)
(data["confirmed"].rolling(5).mean() / data["test"].rolling(5).mean()).plot(ax=ax, kind="line", linewidth=2, label="SMA(5)", figsize=(16, 9))
(data["confirmed"].rolling(10).mean() / data["test"].rolling(10).mean()).plot(ax=ax, kind="line", color="darkblue", linewidth=2, label="SMA(10)", figsize=(16, 9))
plt.legend()
plt.tight_layout()
plt.title("MA of Positive Rate", size=18)
# Get the positive rate since May
fig, ax = plt.subplots(1, 1)
(data["2020-05":]["confirmed"].rolling(5).mean() / data["2020-05":]["test"].rolling(5).mean()).plot(ax=ax, kind="line", linewidth=2, label="SMA(5)", figsize=(16, 9))
(data["2020-05":]["confirmed"].rolling(10).mean() / data["2020-05":]["test"].rolling(10).mean()).plot(ax=ax, kind="line", color="darkblue", linewidth=2, label="SMA(10)", figsize=(16, 9))
data["2020-05":]["positive_rate"].plot(ax=ax, kind="line", color="magenta", linewidth=2, label="Today", figsize=(16, 9))
plt.legend()
plt.tight_layout()
plt.title("Positive Rate since May", size=18)
6.6) Stationarity Testing ¶
# Plot a histogram of the selected data again
subdata = data["2020-05":]
mu = subdata["confirmed"].mean()
sigma = subdata["confirmed"].std()
r_range = np.linspace(subdata["confirmed"].min(), subdata["confirmed"].max(), 10000)
norm_pdf = scs.norm.pdf(r_range, loc=mu, scale=sigma)
fig = plt.figure(figsize=(16, 9))
plt.hist(subdata["confirmed"], bins=30, color="darkblue", alpha=0.7, density=True)
plt.plot(r_range, norm_pdf, color="darkred", label=f"N({mu: .2f}, {sigma: .2f}$^2$)", lw=4)
plt.xlabel("Confirmed Cases Since May", fontsize=14)
plt.ylabel("Probability Density", fontsize=14)
plt.title("Confirmed Cases Histogram Since May", fontsize=24)
plt.legend(loc=(0.6, 0.6), fontsize=16)
plt.tight_layout()
plt.show()
# Get the 3rd and 4th Moment
print("Skewness: {:.2f}".format(scs.skew(subdata["confirmed"])))
print("Extra kurtosis: {:.2f}".format(scs.kurtosis(subdata["confirmed"])))
The daily confirmed cases in the selected period is not significantly skewed. The distribution is platykurtic. Overall, it suffices to say that normal approximation is a fair approximation of the data and no additional scaling steps (taking log, etc.) are needed at this point.
# Autocorrelation Functions
fig, ax = plt.subplots(2, 1, figsize=(16, 9))
plot_acf(subdata["confirmed"], ax=ax[0], lags=15, alpha=0.05)
plot_pacf(subdata["confirmed"], ax=ax[1], lags=15, alpha=0.05)
plt.tight_layout()
plt.show()
The autocorrelation gradually descreases with time lag and it becomes insignificant beyond lag-4. The PACF indicates that a first-order autoregressive model AR(1) may be plausible to explain correlations as such.
def adf_test(ts):
indices = ["Augmented Dickey-Fuller statistic", "p-value", "# of lags used", "# of observations used"]
adf_val = adfuller(ts, autolag="AIC")
critical_val = pd.Series(adf_val[:4], index=indices)
for pct, val in adf_val[4].items():
critical_val[f"Critical Value ({pct})"] = val
return critical_val
def kpss_test(ts, h0_type="c"):
indices = ["Kwiatkowski-Phillips-chmidt-Shin statistic", "p-value", "# of lags"]
kpss_val = kpss(ts, regression=h0_type)
critical_val = pd.Series(kpss_val[:3], index=indices)
for pct, val in kpss_val[3].items():
critical_val[f"Critical Value ({pct})"] = val
return critical_val
print(adf_test(subdata["confirmed"]))
print(kpss_test(subdata["confirmed"]))
The ADF and KPSS tests both imply that the selected data is about stationary at 5% significance level.
6.7) Seasonal Decomposition ¶
result = seasonal_decompose(subdata["confirmed"], model="multiplicative")
fig, ax = plt.subplots(4, 1, sharex=True, figsize=(16, 9))
result.observed.plot(ax=ax[0])
ax[0].set(title="Seasonal Decomposition of Confirmed Cases", ylabel="Observed", )
result.trend.plot(ax=ax[1])
ax[1].set(ylabel="Trend")
result.seasonal.plot(ax=ax[2])
ax[2].set(ylabel="Seasonal")
result.resid.plot(ax=ax[3])
ax[3].set(ylabel="Residual")
plt.tight_layout()
plt.show()
result = seasonal_decompose(subdata["confirmed"].rolling(5).mean().dropna(), model="multiplicative")
fig, ax = plt.subplots(4, 1, sharex=True, figsize=(16, 9))
result.observed.plot(ax=ax[0])
ax[0].set(title="Seasonal Decomposition of Confirmed Cases SMA(5)", ylabel="Observed", )
result.trend.plot(ax=ax[1])
ax[1].set(ylabel="Trend")
result.seasonal.plot(ax=ax[2])
ax[2].set(ylabel="Seasonal")
result.resid.plot(ax=ax[3])
ax[3].set(ylabel="Residual")
plt.tight_layout()
plt.show()
6.8) ARIMA Modelling ¶
train = subdata["confirmed"][:45]
test = subdata["confirmed"][45:]
model = pm.auto_arima(subdata["confirmed"].dropna(), stepwise=True, error_action="ignore", support_warnings=True, n_jobs=-1)
model.summary()
model.fit(train)
pred = model.predict(n_periods=16)
forecast = pd.DataFrame(pred, index=test.index, columns=["Prediction"])
pd.concat([subdata["confirmed"], forecast], axis=1).plot(figsize=(16, 9), title="AutoARIMA Model")
train_smooth = train.rolling(5).mean() / train.rolling(5).std()
total_smooth = subdata["confirmed"].rolling(5).mean() / subdata["confirmed"].rolling(5).std()
model = ARIMA(train_smooth.dropna(), order=(2, 0, 2)).fit(disp=0)
model.summary()
pred = model.forecast(16, alpha=0.2)
forecast = [pd.DataFrame(pred[0], columns=["prediction"]), pd.DataFrame(pred[2], columns=["ci_lower", "ci_upper"])]
forecast = pd.concat(forecast, axis=1).set_index(test.index)
fig, ax = plt.subplots(1, figsize=(16, 9))
ax = sns.lineplot(data=total_smooth, color="slateblue", label="actural")
ax.plot(forecast.prediction, c="darkblue", label="ARMA(2, 2)")
ax.fill_between(forecast.index, forecast.ci_lower, forecast.ci_upper, alpha=0.2, facecolor="darkblue")
ax.set(title="ARMA(2,2) with SMA(5) and NORM(5) Smoothing")
plt.legend()
plt.tight_layout()
plt.show()
6.9) ETS Modelling ¶
model1 = Holt(train).fit()
model2 = Holt(train, exponential=True).fit()
pred1 = model1.forecast(16)
pred2 = model2.forecast(16)
fig, ax = plt.subplots(1, figsize=(16, 9))
subdata["confirmed"].plot(color="slateblue", label="Actural", legend=True, title="Holt-Winters Model")
pred1.plot(color="darkblue", legend=True, label="Linear Trend")
pred2.plot(color="magenta", legend=True, label="Exponential Trend")
plt.show()
model3 = ExponentialSmoothing(train, trend="mul", seasonal="add", seasonal_periods=3).fit()
pred3 = model3.forecast(16)
fig, ax = plt.subplots(1, figsize=(16, 9))
subdata["confirmed"].plot(color="slateblue", label="Actural", legend=True, title="Holt-Winters Model")
pred3.plot(color="darkblue", legend=True, label="Holt-Winters Seasonal Model")
plt.show()
6.10) Facebook Prophet ¶
model = Prophet()
model.fit(train.reset_index(drop=False).rename(columns={"date": "ds", "confirmed": "y"}))
period_pred = model.make_future_dataframe(periods=16)
pred = model.predict(period_pred)
model.plot(pred)
plt.title("Facebook Prophet Model")
plt.show()
The model is not a good fit afterall.
def split_sequence(sequence, n_steps):
X, y = list(), list()
for i in range(len(sequence)):
# find the end of this pattern
end_ix = i + n_steps
# check if we are beyond the sequence
if end_ix > len(sequence)-1:
break
# gather input and output parts of the pattern
seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y)
n_steps = 4
X, y = split_sequence(train, n_steps)
for i in range(len(X)):
print(X[i], y[i])
n_features = 1
X = X.reshape((X.shape[0], X.shape[1], n_features))
model = Sequential()
model.add(LSTM(50, activation="relu", input_shape=(n_steps, n_features)))
model.add(Dense(1))
model.compile(optimizer="adam", loss="mse")
model.fit(X, y, epochs=100, verbose=1)
X_pred, y_test = split_sequence(subdata["confirmed"][42:], n_steps)
X_pred = X_pred.reshape((X_pred.shape[0], X_pred.shape[1], n_features))
y_pred = model.predict(X_pred)
y_pred
forecast = pd.DataFrame(y_pred.reshape(-1), index=test.index[1:], columns=["Prediction"])
pd.concat([subdata["confirmed"], forecast], axis=1).plot(figsize=(16, 9), title="LSTM Model")
While some moves have been predicted correctly, some have totally gone to the wrong direction. We do not have enough evidence to justify the forecast as a whole.
7) TimeAge ¶
timeAgeData = pd.read_csv('covid/timeage.csv')
display(timeAgeData.head())
fig = px.line(timeAgeData, x="date", y="confirmed", color='age', title="Confirmed cases of various age group over time")
fig.update_layout(hovermode='x')
fig.show()
timeAgeData = pd.read_csv('covid/timeage.csv')
fig = px.line(timeAgeData, x="date", y="deceased", color='age', title="Deceased cases of various age group over time")
fig.update_layout(hovermode='x')
fig.show()
7.1) Deceased vs confirmed cases across different age group over time ¶
timeAgeData = pd.read_csv('covid/timeage.csv')
timeAgeData['month'] = pd.to_datetime(timeAgeData['date']).dt.month
display(timeAgeData.head())
fig = px.scatter(timeAgeData,
x='confirmed',
y='deceased',
color="age",
size_max=100,
size="deceased",
animation_frame="date",
animation_group="age",
range_x=[0, timeAgeData['confirmed'].max()],
range_y=[0, timeAgeData['deceased'].max() + timeAgeData['deceased'].std()]
)
fig.layout.updatemenus[0].buttons[0].args[1]["frame"]["duration"] = 200
fig.layout.updatemenus[0].buttons[0].args[1]["transition"]["duration"] = 200
fig.layout.coloraxis.showscale = False
fig.layout.sliders[0].pad.t = 10
fig.layout.updatemenus[0].pad.t= 10
fig.show()
Lets have a closer look by splitting the age group into different group¶
display(timeAgeData.head())
timeAgeData = timeAgeData[~timeAgeData['age'].isin(['0s','10s','20s'])]
timeAgeData['month'] = pd.to_datetime(timeAgeData['date']).dt.month
fig = px.scatter(timeAgeData, x="confirmed", y="deceased", animation_frame="date", animation_group="age",
size="deceased", color="age", hover_name="age", facet_col="age",
range_x=[0, timeAgeData['confirmed'].max()],
range_y=[0, timeAgeData['deceased'].max()])
fig.show()
7.2) Testing of Homogeneous Mortality Hypothesis ¶
Mortality Rates across Age Groups¶
timeage = pd.read_csv("covid/timeAge.csv")
timeage.head()
timeagegrouped = timeage.groupby("age")["confirmed", "deceased"].sum()
timeagegrouped
Single-Factor ANOVA: $H_0: p_{00}=p_{10}=p_{20}=...=p_{80}=p_I$ ; $H_a$: At least two being unequal
p = timeagegrouped["deceased"] / timeagegrouped["confirmed"]
p.plot(kind="barh", figsize=(16, 9))
p_I = p.mean()
SSTr = np.sum([(n*(x-p_I))**2 for x, n in zip(p, timeagegrouped["confirmed"])])
SSE = np.sum([x*(1-x)*n for x, n in zip(p, timeagegrouped["confirmed"])])
df = np.sum([n-1 for n in timeagegrouped["confirmed"]])
F = (SSTr/(len(p))) / (SSE/df)
F
The F ratio is huge, which implies that the treatment groups differentiate mortality rates significantly. More specifically, older age groups tend to have higher mortality rates, which is consistent with the observation from the horizontal bar chart.
7.3) Does TimeAge Dataset tallies with the patient.csv ?¶
age = pd.read_csv("covid/TimeAge.csv")
age.date = age.date.apply(lambda x: pd.to_datetime(x))
age_latest = age[age.date == max(age.date)]
age_latest
sns.barplot( x = "age", y = "confirmed", data = age_latest)
plt.title("Latest number of confirmed cases as of 30th June 2020", size = 15)
plt.tick_params(axis = "both", labelsize = 15)
This tallies with the patient.csv although the patient.csv is not complete.¶
7.4) Deceased Rate ¶
age["deceased rate"] = age.deceased/age.confirmed * 100.0
plt.figure(figsize = (16,10))
for group in age.groupby("age"):
plt.plot(group[1].date.values, group[1]["deceased rate"].values, label = group[0])
plt.xticks(rotation = 90)
plt.title("Deceased Rate over time", size = 15)
plt.ylabel("Deceased Rate %", size = 15)
plt.xlabel("Date", size = 15)
plt.legend()
plt.show()
As time goes by, the elderly age group deceased rate has spiked up rapidly
8) Time Gender ¶
timeGender = pd.read_csv('covid/timegender.csv')
display(timeGender.head())
fig = px.line(timeGender, x="date", y="confirmed", color='sex', title="Confirmed cases between genders over time")
fig.update_layout(hovermode='x')
fig.show()
fig = px.line(timeGender, x="date", y="deceased", color='sex', title="Deceased cases between genders over time")
fig.update_layout(hovermode='x')
fig.show()
8.1) Deceased vs confirmed cases across different gender over time ¶
timeGender = pd.read_csv('covid/timegender.csv')
display(timeGender.head())
fig = px.scatter(timeGender,
x='confirmed',
y='deceased',
color="sex",
size_max=100,
size="deceased",
animation_frame="date",
animation_group="sex",
range_x=[0, timeGender['confirmed'].max() + timeGender['confirmed'].std()],
range_y=[0, timeGender['deceased'].max() + timeGender['deceased'].std()]
)
fig.layout.updatemenus[0].buttons[0].args[1]["frame"]["duration"] = 200
fig.layout.updatemenus[0].buttons[0].args[1]["transition"]["duration"] = 200
fig.layout.coloraxis.showscale = False
fig.layout.sliders[0].pad.t = 10
fig.layout.updatemenus[0].pad.t= 10
fig.show()
8.2) Confirmed cases daily average increase amount by month (Sort by gender) ¶
timeGender = pd.read_csv('covid/timegender.csv')
timeGenderAnalysis = timeGender.copy()
timeGenderAnalysis['confirmed increase'] = timeGenderAnalysis['confirmed'] - timeGenderAnalysis['confirmed'].shift(2)
timeGenderAnalysis['deceased increase'] = timeGenderAnalysis['deceased'] - timeGenderAnalysis['deceased'].shift(2)
timeGenderAnalysis['month'] = pd.to_datetime(timeGenderAnalysis['date']).dt.month
timeGenderAnalysis['day'] = pd.to_datetime(timeGenderAnalysis['date']).dt.day_name()
timeGenderAnalysisMonth = timeGenderAnalysis.groupby(['month','sex'])['confirmed increase'].mean()
timeGenderAnalysisMonth = timeGenderAnalysisMonth.reset_index()
timeGenderAnalysisMonthMelted = pd.melt(timeGenderAnalysisMonth, id_vars=['month','sex'], value_vars=['confirmed increase'])
display(timeGenderAnalysisMonthMelted.head())
fig = px.bar(timeGenderAnalysisMonthMelted, x='month', y='value', color='sex', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
8.3) Confirmed cases daily average increase amount by day (Sort by gender) ¶
timeGenderAnalysisMonth = timeGenderAnalysis.groupby(['day','sex'])['confirmed increase'].mean()
timeGenderAnalysisMonth = timeGenderAnalysisMonth.reset_index()
weekdays = ["Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday", "Sunday"]
timeGenderAnalysisMonth['day'] = pd.Categorical(timeGenderAnalysisMonth['day'],categories=weekdays)
timeGenderAnalysisMonth = timeGenderAnalysisMonth.sort_values('day')
timeGenderAnalysisMonthMelted = pd.melt(timeGenderAnalysisMonth, id_vars=['day','sex'], value_vars=['confirmed increase'])
display(timeGenderAnalysisMonthMelted.head())
fig = px.bar(timeGenderAnalysisMonthMelted, x='day', y='value', color='sex', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
8.4) Deceased cases daily average increase amount by month (Sort by gender) ¶
timeGenderAnalysisMonth = timeGenderAnalysis.groupby(['month','sex'])['deceased increase'].mean()
timeGenderAnalysisMonth = timeGenderAnalysisMonth.reset_index()
timeGenderAnalysisMonthMelted = pd.melt(timeGenderAnalysisMonth, id_vars=['month','sex'], value_vars=['deceased increase'])
display(timeGenderAnalysisMonthMelted.head())
fig = px.bar(timeGenderAnalysisMonthMelted, x='month', y='value', color='sex', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
8.5) Deceased cases daily average increase amount by day (Sort by gender) ¶
timeGenderAnalysisMonth = timeGenderAnalysis.groupby(['day','sex'])['deceased increase'].mean()
timeGenderAnalysisMonth = timeGenderAnalysisMonth.reset_index()
weekdays = ["Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday", "Sunday"]
timeGenderAnalysisMonth['day'] = pd.Categorical(timeGenderAnalysisMonth['day'],categories=weekdays)
timeGenderAnalysisMonth = timeGenderAnalysisMonth.sort_values('day')
timeGenderAnalysisMonthMelted = pd.melt(timeGenderAnalysisMonth, id_vars=['day','sex'], value_vars=['deceased increase'])
display(timeGenderAnalysisMonthMelted.head())
fig = px.bar(timeGenderAnalysisMonthMelted, x='day', y='value', color='sex', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
8.6) Mortality Rates across Gender Groups ¶
timegender = pd.read_csv("covid/timeGender.csv")
timegender.head()
timegendergrouped = timegender.groupby("sex")["confirmed", "deceased"].sum()
timegendergrouped
z Test: $H_0: p_m=p_f$; $H_0: p_m\neq p_f$
p = timegendergrouped["deceased"] / timegendergrouped["confirmed"]
p.plot(kind="barh", figsize=(16, 9))
z = (p["male"] - p["female"]) / np.sqrt(p["male"]*(1-p["male"])/timegendergrouped["confirmed"]["male"]+p["female"]*(1-p["female"])/timegendergrouped["confirmed"]["female"])
z
The staggering z score indicates that mortality rate also varies between genders. More specifically, males are far more vulnerable to COVID-led mortality than females.
9) Time Province ¶
timeProvince = pd.read_csv('covid/timeprovince.csv')
display(timeProvince.head())
fig = px.line(timeProvince, x="date", y="confirmed", color='province', title="Confirmed cases of various province over time")
fig.update_layout(hovermode='x')
fig.show()
fig = px.line(timeProvince, x="date", y="released", color='province', title="Released cases of various province over time")
fig.update_layout(hovermode='x')
fig.show()
fig = px.line(timeProvince, x="date", y="deceased", color='province', title="Deceased cases of various province over time")
fig.update_layout(hovermode='x')
fig.show()
9.1) Deceased vs confirmed cases across different province over time (With Daegu) ¶
timeProvince = pd.read_csv('covid/timeprovince.csv')
display(timeProvince.head())
fig = px.scatter(timeProvince,
y='released',
x='confirmed',
color="province",
size_max=100,
size="deceased",
animation_frame="date",
animation_group="province",
range_y=[0, timeProvince['confirmed'].max() + timeProvince['confirmed'].std()],
range_x=[0, timeProvince['released'].max() + timeProvince['released'].std()]
)
fig.layout.updatemenus[0].buttons[0].args[1]["frame"]["duration"] = 200
fig.layout.updatemenus[0].buttons[0].args[1]["transition"]["duration"] = 200
fig.layout.coloraxis.showscale = False
fig.layout.sliders[0].pad.t = 10
fig.layout.updatemenus[0].pad.t= 10
fig.show()
9.2) Deceased vs confirmed cases across different province over time (Without Daegu) ¶
timeProvince = pd.read_csv('covid/timeprovince.csv')
timeProvince = timeProvince[timeProvince['province'] != 'Daegu']
display(timeProvince.head())
fig = px.scatter(timeProvince,
y='released',
x='confirmed',
color="province",
size_max=100,
size="deceased",
animation_frame="date",
animation_group="province",
range_y=[0, timeProvince['confirmed'].max() + timeProvince['confirmed'].std()],
range_x=[0, timeProvince['released'].max() + timeProvince['released'].std()]
)
fig.layout.updatemenus[0].buttons[0].args[1]["frame"]["duration"] = 200
fig.layout.updatemenus[0].buttons[0].args[1]["transition"]["duration"] = 200
fig.layout.coloraxis.showscale = False
fig.layout.sliders[0].pad.t = 10
fig.layout.updatemenus[0].pad.t= 10
fig.show()
9.3) Mortality Rates across Provinces ¶
timeprovince = pd.read_csv("covid/timeProvince.csv")
timeprovince.head()
timeprovincegrouped = timeprovince.groupby("province")["confirmed", "deceased"].sum()
timeprovincegrouped
p = timeprovincegrouped["deceased"] / timeprovincegrouped["confirmed"]
p.plot(kind="barh", figsize=(16, 9))
p_I = p.mean()
SSTr = np.sum([(n*(x-p_I))**2 for x, n in zip(p, timeprovincegrouped["confirmed"])])
SSE = np.sum([x*(1-x)*n for x, n in zip(p, timeprovincegrouped["confirmed"])])
df = np.sum([n-1 for n in timeprovincegrouped["confirmed"]])
F = (SSTr/(len(p))) / (SSE/df)
F
Once again, province treatment groups seem to explain mortality differentials well as F ratio is greater than 1 at any reasonable significance level.
9.4) Does TimeProvince Dataset tallies with the cases.csv & patient.csv?¶
province = pd.read_csv("covid/TimeProvince.csv")
province.date = province.date.apply(lambda x: pd.to_datetime(x))
province_latest = province[province.date == max(province.date)]
province_latest.head()
province_latest.confirmed.sum()
plt.figure(figsize = (14,12))
sns.barplot( x = "province", y = "confirmed", data = province_latest)
plt.title("Latest number of confirmed cases as of 30th June 2020", size = 15)
plt.tick_params(axis = "both", labelsize = 15, labelrotation = 90)
plt.show()
TimeProvince Dataset tallies with the cases.csv, not with the patient.csv¶
10) In depth Analysis Of Daegu Cases using Technical Analysis. ¶
timeProvince = pd.read_csv('covid/timeprovince.csv')
dataForDaegu = timeProvince[timeProvince['province'] == 'Daegu']
dataForDaegu = dataForDaegu[['date','province','confirmed']]
dataForDaegu['increasePerDay'] = dataForDaegu['confirmed'] - dataForDaegu['confirmed'].shift(1)
dataForDaegu = dataForDaegu[['date','province','increasePerDay']]
dataForDaegu = dataForDaegu.rename({'increasePerDay':'Increase Per Day'}, axis=1)
display(dataForDaegu.head())
fig = px.line(dataForDaegu, x="date", y="Increase Per Day", title="Daegu Cases Per Day")
fig.update_layout(hovermode='x')
fig.show()
Daeugu's Cases is most active during Feb to Apr period.
10.1) Technical Analysis ¶
# Uncommend to focus data on active period
# dataForDaegu = dataForDaegu.set_index('date')
# dataForDaegu = dataForDaegu['2020-02-01' : '2020-04-31'].reset_index()
dataForDaegu['10 Days Moving Average'] = dataForDaegu['Increase Per Day'].rolling(10).mean()
dataForDaegu['Upper Limit 10 day Bollinger Band'] = dataForDaegu['Increase Per Day'].rolling(10).mean() + (dataForDaegu['Increase Per Day'].rolling(10).std() * 2)
dataForDaegu['Lower Limit 10 day Bollinger Band'] = dataForDaegu['Increase Per Day'].rolling(10).mean() - (dataForDaegu['Increase Per Day'].rolling(10).std() * 2)
dataForDaeguNew = pd.melt(dataForDaegu, id_vars=['date'], value_vars=['Increase Per Day', '10 Days Moving Average','Upper Limit 10 day Bollinger Band','Lower Limit 10 day Bollinger Band'])
display(dataForDaeguNew.head())
fig = px.line(dataForDaeguNew, x="date", y="value", color='variable', title="Daegu Cases Per Day")
fig['data'][2]['line']['color']="rgba(147,212,219,0.8)"
fig['data'][3]['line']['color']="rgba(157,212,219,0.8)"
fig.update_layout(hovermode='x')
fig.show()
10.2) Stats By Month ¶
dataForDaeguNew['date'] = pd.to_datetime(dataForDaeguNew['date'])
dataForDaeguNew['Month'] = dataForDaeguNew['date'].dt.month
dataForDaeguNew['Day'] = dataForDaeguNew['date'].dt.day_name()
dataForDaeguMonth = dataForDaeguNew[['variable','Month']]
dataForDaeguMonth = dataForDaeguNew.groupby(['Month','variable'])['value'].mean()
dataForDaeguMonth = dataForDaeguMonth.reset_index()
display(dataForDaeguMonth.head())
fig = px.bar(dataForDaeguMonth, x='Month', y='value', color='variable', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
Stats By Day ¶
dataForDaeguMonth = dataForDaeguNew[['variable','Day']]
dataForDaeguMonth = dataForDaeguNew.groupby(['Day','variable'])['value'].mean()
dataForDaeguMonth = dataForDaeguMonth.reset_index()
weekdays = ["Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday", "Sunday"]
dataForDaeguMonth['Day'] = pd.Categorical(dataForDaeguMonth['Day'],categories=weekdays)
dataForDaeguMonth = dataForDaeguMonth.sort_values('Day')
display(dataForDaeguMonth.head())
fig = px.bar(dataForDaeguMonth, x='Day', y='value', color='variable', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
11) Time Series World Map Visualisation of COVID-19 cases in korea ¶
timeProvince = pd.read_csv('covid/timeprovince.csv')
data = {'province': ['Seoul', 'Busan', 'Daegu', 'Incheon', 'Gwangju', 'Daejeon',
'Ulsan', 'Sejong', 'Gyeonggi-do', 'Gangwon-do',
'Chungcheongbuk-do', 'Chungcheongnam-do', 'Jeollabuk-do',
'Jeollanam-do', 'Gyeongsangbuk-do', 'Gyeongsangnam-do', 'Jeju-do'],
'longitude': [127.047325,129.066666,128.600006,126.705208,126.916664,127.385002,
129.316666,127.2822,127.143738,127.920158,
127.935905,126.979874,126.916664,126.9910,
129.263885,128.429581,126.5312],
'latitude': [37.517235,35.166668,35.866669,37.456257,35.166668,36.351002,
35.549999,36.4870,37.603405,37.342220,
36.981304,36.806702,35.166668,34.8679,
35.835354,34.855228,33.4996]}
location = pd.DataFrame(data=data)
mergedData = timeProvince.merge(location, on='province', how='left')
mergedData = mergedData.dropna()
mergedData.head()
11.1) With Animation ¶
fig = px.scatter_mapbox(
mergedData, lat="latitude", lon="longitude",
size="confirmed", size_max=100,
color="deceased", color_continuous_scale=px.colors.sequential.Burg,
hover_name="province",
mapbox_style='dark', zoom=6,
animation_frame="date", animation_group="province"
)
fig.layout.updatemenus[0].buttons[0].args[1]["frame"]["duration"] = 200
fig.layout.updatemenus[0].buttons[0].args[1]["transition"]["duration"] = 200
fig.layout.coloraxis.showscale = False
fig.layout.sliders[0].pad.t = 10
fig.layout.updatemenus[0].pad.t= 10
fig.show()
11.2) Without animation ¶
fig = px.scatter_mapbox(
mergedData, lat="latitude", lon="longitude",
size="confirmed", size_max=100,
color="deceased", color_continuous_scale=px.colors.sequential.Burg,
hover_name="province",
mapbox_style='dark', zoom=6,
)
fig.show()
12) Weather ¶
weatherData = pd.read_csv('covid/weather.csv')
weatherData = weatherData.set_index('date')
weatherData = weatherData['2020-01-01' : '2020-08-31'].reset_index()
display(weatherData.head())
weatherDataForHeatmap = weatherData.pivot("date", "province", "avg_temp")
f, ax = plt.subplots(figsize=(20, 20))
sns.heatmap(weatherDataForHeatmap, cmap="RdPu", annot=False, fmt="d", linewidths=.5, ax=ax).set_title('Weather Over Time')
12.1) Busan Avg Temp (Mean) vs Most Wind Direction (Mean) Analysis ¶
high_direction_province = weatherData.copy()
high_direction_province['month'] = high_direction_province['date'].apply(pd.to_datetime).dt.month
high_direction_province.head()
high_direction_province_grouped = high_direction_province.groupby(['province','month']).agg({'avg_temp':['mean','std','min','max'],
'min_temp':['mean','std'],
'max_temp':['mean','std'],
'max_wind_speed':['mean','std'],
'most_wind_direction':['mean','std'],
'avg_relative_humidity':['mean','std']})
print('Agg Data')
display(high_direction_province_grouped.head())
high_direction_province_grouped = high_direction_province_grouped.stack().stack()
high_direction_province_grouped = high_direction_province_grouped.reset_index()
high_direction_province_grouped.columns = ['Province','Month', 'Measurement Type','Weather Type','Value']
high_direction_province_grouped = high_direction_province_grouped.set_index(['Weather Type','Measurement Type','Province','Month'])
print('Indexed Data')
display(high_direction_province_grouped.head())
busan_data = high_direction_province_grouped.loc[(['avg_temp','most_wind_direction'],slice(None),'Busan'), :].sort_values(['Weather Type','Month'])
busan_data.head()
busan_data_mean = high_direction_province_grouped.loc[(['avg_temp','most_wind_direction'],'mean','Busan'), :].sort_values(['Weather Type','Month']).reset_index()
display(busan_data_mean.head())
fig = px.bar(busan_data_mean, x='Month', y='Value', color='Weather Type', barmode='group')
fig.update_layout(hovermode='x')
fig.show()
busan_temp = busan_data_mean[busan_data_mean['Weather Type'] == 'avg_temp']['Value']
busan_temp = pd.DataFrame(busan_temp).reset_index().drop('index',axis=1)
busan_temp.columns = ['avg_temp']
# display(busan_temp)
busan_wind_direction = busan_data_mean[busan_data_mean['Weather Type'] == 'most_wind_direction']['Value']
busan_wind_direction = pd.DataFrame(busan_wind_direction).reset_index().drop('index',axis=1)
busan_wind_direction.columns = ['most_wind_direction']
# display(busan_wind_direction)
plot_table = busan_wind_direction.join(busan_temp)
display(plot_table)
fig = px.scatter(plot_table, x="most_wind_direction", y="avg_temp", trendline="ols", title="Avg Temp & Wind Direction")
fig.update_layout(hovermode='x')
fig.show()
With a R squared of 0.79, there is a strong correlation between the avg-temp and the most wind direction.
The wind direction increases whether there is a decrease in temperature
12.2) Does other region has the same relationship between avg_temp and most_wind direction? ¶
all_data = high_direction_province_grouped.loc[(['avg_temp','most_wind_direction'],'mean',slice(None),slice(None)), :].sort_values(['Weather Type','Month'])
all_data = all_data.reset_index()
all_data_temp = all_data[all_data['Weather Type'] == 'avg_temp']['Value']
all_data_temp = all_data_temp.reset_index()
all_data_temp = all_data_temp.drop('index',axis=1)
all_data_temp.columns = ['temp']
# all_data_temp.head()
all_data_wind = all_data[all_data['Weather Type'] == 'most_wind_direction']['Value']
all_data_wind = all_data_wind.reset_index()
all_data_wind = all_data_wind.drop('index',axis=1)
all_data_wind.columns = ['wind']
# all_data_wind.head()
all_data_plot = all_data_temp.join(all_data_wind)
display(all_data_plot.head())
fig = px.scatter(all_data_plot, x="wind", y="temp", trendline="ols", title="Avg Temp & Wind Direction")
fig.update_layout(hovermode='x')
fig.show()
With a R squared of 0.009, it seems that other region does not follow similar trend as Busan.
13) Region ¶
13.1) Number of nusing home and elder population ratio across Korea ¶
regionData = pd.read_csv('covid/region.csv')
pd.set_option('display.max_rows', regionData.shape[0]+1)
display(regionData.head())
fig = px.scatter_mapbox(
regionData[regionData.city != 'Korea'],
text="city",
lat="latitude",
lon="longitude",
color="elderly_population_ratio",
size="nursing_home_count",
color_continuous_scale=px.colors.sequential.Burg,
size_max=100,
zoom=6,
title="Number of nusing home and elder population ratio across Korea")
fig.show()
13.2) Correlation between elder population ratio and number of cases ¶
region = pd.read_csv("covid/Region.csv")
region.head()
region_elderly_mean = pd.DataFrame(region[region.province != "Korea"].groupby("province")["elderly_population_ratio"].mean().sort_values(ascending = False))
region_elderly_mean.head()
plt.figure(figsize = (13,10))
sns.barplot(x = region_elderly_mean.index, y = region_elderly_mean["elderly_population_ratio"], palette = "muted")
plt.tick_params(axis = "both", labelsize = 15, rotation = 90)
plt.title("Elderly population by province", size = 15)
plt.ylabel("Elderly Population Ratio", size = 15)
plt.xlabel("Province", size = 15)
plt.show()
province_latest.sort_values("confirmed", ascending = False, inplace = True)
region_elderly_mean.loc[province_latest.province,:].head()
region_elderly_mean.loc[province_latest.province,:]
plt.figure(figsize = (13,10))
sns.barplot(x = region_elderly_mean.loc[province_latest.province,:].index,
y = region_elderly_mean.loc[province_latest.province,"elderly_population_ratio"], palette = "muted")
plt.tick_params(axis = "both", labelsize = 15, rotation = 90)
plt.title("Elderly population by province (order by the number of confirmed cases - Descending Order)", size = 15)
plt.ylabel("Elderly Population Ratio", size = 15)
plt.xlabel("Province", size = 15)
plt.show()
Seems like the elderly population by province is not correlated with the number of confirmed cases¶
14) Web Scalping: Comparsion across the world ¶
page = requests.get("https://www.worldometers.info/coronavirus")
page.status_code
# page.content
soup = BeautifulSoup(page.content, 'lxml')
# print(soup.prettify())
covidTable = soup.find('table', attrs={'id': 'main_table_countries_today'})
# covidTable
14.1) Getting the data from the table ¶
rows = covidTable.find_all("tr", attrs={"style": ""})
covidData = []
for i,data in enumerate(rows):
if i == 0:
covidData.append(data.text.strip().split("\n")[:13])
else:
covidData.append(data.text.strip().split("\n")[:12])
# covidData
14.2) Covert to data ¶
covidTable = pd.DataFrame(covidData[1:], columns=covidData[0][:12])
covidTable = covidTable[~covidTable['#'].isin(['World', 'Total:'])]
covidTable = covidTable.drop('#', axis =1)
covidTable.head()
14.3) Worldwide Total Cases Chart ¶
fig = px.bar(covidTable, y='TotalCases', x='Country,Other')
fig.update_layout(hovermode='x')
fig.show()
We will be using log because the data is highly skewed
covidTable['logTotalCases'] = np.log(covidTable['TotalCases'].str.replace(r'\D', '').astype(int))
covidTable = covidTable.sort_values(by=['logTotalCases'])
fig = px.bar(covidTable, y='logTotalCases', x='Country,Other')
fig.update_layout(hovermode='x')
fig.show()
14.4) Worldwide Total Death Chart ¶
pd.set_option('display.max_rows', covidTable.shape[0]+1)
covidTable['TotalDeaths'].str.strip()
covidTable['TotalDeaths'].replace('', np.nan, inplace=True)
covidTable['TotalDeaths'].replace(' ', np.nan, inplace=True)
covidTable['TotalDeaths'] = covidTable['TotalDeaths'].fillna(0)
covidTable['logTotalDeath'] = np.log(covidTable['TotalDeaths'].str.replace(r'\D', '').astype(float))
covidTable = covidTable.sort_values(by=['logTotalDeath'])
display(covidTable.head())
fig = px.bar(covidTable, y='logTotalDeath', x='Country,Other')
fig.update_layout(hovermode='x')
fig.show()
14.5) Scatterplot between total cases and total death ¶
fig = px.scatter(covidTable, x="logTotalDeath", y="logTotalCases", trendline="ols", title="Total Cases againist Total Death (Log)")
fig.update_layout(hovermode='x')
fig.show()
With a R squared value of 0.88, there is a strong correlation between the cases and the deaths.
The more cases there are, the higher the amount of death
15) Summarise Key findings from Exploratory Data Analysis ¶
15.1) Overall Cases in Korea ¶
- On average, there are 100 COVID-19 cases in infected city.
- The numbers are highly skewed by Nam-gu, a province of Daegu. Nam-gu has about 4500 cases.
- Most of the clusters are in the province of Daegu, Gyeonggi-do and Seoul
Cases across various Korea province¶
- Majority of the province has more individual cases of COVID-19 than group cases with the exception of Incheon and Ulsan
- Seoul, Daegu, Gyeonggi-do and Gyeongsangbuk-do has the most number of individual cases among the Korea provinces, number of cases range from 150 to 200 with the exception of Daegu
- In addition, the same group of provinces has the most number of grouped cases, number of cases range from 50-100 with the exception of Daegu
Source of infection¶
- Sources of infection mainly come from Shincheonji Church, Itawon Clubs, Contact with Patients and Overseas inflow
- Most of the infection sources across various province has less than 500 cases with the exception of Daegu.
- Daegu has more than 4000 cases from Shincheonji Church and about 2000 cases from contact with patient and other cases each.
15.2) Patient Cases ¶
- There is a quick spike in daily COVID-19 cases from Feb to Mar before slowing dripping down to single digit in May. There are double digit COVID-19 cases in June
Recovery Speed¶
- Age has an R-squared value of 0.04 for male and 0.03 for female against total treatment days.
- At first graze, age seems to have little to no effect on recovery speed.
- However when we used the mean recovery days for each age group, it was found that younger people recovered fast from COVID-19 as compared to older people.
- Average days to recover for young people (<=30) is around 25 days and below. Middle-aged people(30-60) took about 25-30 days to recover. Older people (>=70) took about 32-36 days to recover
- Interestingly, infected people in Daegu only conist of people from 50s to 70s. In addition, it took less than 15 days to recover. People in Jeollabuk-do take longer to recover from COVID-19 as compared to the rest of the provinces. Majority of the people took about 20-25 days to recover.
Fatality Speed¶
- The average number of treatment day a patient had before he/she passed away is shorter than the average day it took for a patient recover.
- In addition, younger patient has a lower number of treatment days as compared to older patients. This might indicate that younger patient seek treatment at the later stage of COVID-19.
- Coincidentally, the number of treatment days increased as the age increases. The trend is similar to the recovery speed among during age group.
- Daegu has the fastest fatality speed. An average patient is under treatment for less than 10 days before he/she passed away
- Gyeonggi-do has an outliner. A 30s year old patient died in last than 10 days after seeking treatment.
Percentage of patients recovered, under treatment and deceased¶
- Daegu has the highest fatality amount all the provinces. It has a fatality rate of more than 10%. In addition, Daejeon, Gyeongsangbuk-do and Ulsan are the only provinces which have fatailty.
- Male has a higher fatality rate and a lowest survival rate as compared to female
COVID-19 Tranmission Amount¶
- Majority of the cases only spread to 1 other person.
- Cases #20000000205 is a super spread who spreaded to more than 50 people.
- In addition, there are less than 10 cases where patient spread to more than 30 people or more.
15.3) Policy ¶
- There is a quick spike in daily COVID-19 cases from Feb to Mar before slowing dripping down to single digit in May. There are double digit COVID-19 cases in June
- Technology related policy are introduced in Feb, especially thanks to policy like open data, people like us are able to do analysis on Korea COVID-19 cases.
- After the spike in COVID-19 cases in March, education, social, health and immigration policy are introduced rapidly. Furthermore, the alert level was upgraded to Level 4 red.
- After the introduction of the policies, the number of COVID-19 cases dropped drastically during April and May. Hence the policies are effective.
- However, it seems to be lax in control of COVID-19 cases as the COVID-19 slowly creep up to double digit in May/June. This forced the govtnment to introduced administrative policies such as closure of clubs to control the situation.
15.4) Cases Over Time Analysis ¶
- As for 31st Jun 2020, 1.27 million of people has gone for testing, 1.24 million are tested negative, 12.8 thousand of confirmed cases, 11.5 thousand of released cases and 282 people has passed away.
- Majority of the people are tested negative for covid-19 and less than 1% are tested positive for the virus.
- Among those who are tested positive, almost 90% of the people has recovered and about 2% of the people has passed away
15.5) Cases Over Age & Time Analysis ¶
- Age group in the 20s 40s 50s 60s has higher infection cases as compared to other age group.
- Furthermore, in the deceased section, most of the fatalities are in the age group of 60s 70s 80s,
- This indicate that the risk of death from COVID-19 increases with age.
15.6) Cases Over Gender & Time Analysis ¶
- There are more female infected cases as compared to male cases.
- The rate of increases of confirmed cases are about the same for both gender over the last 6 months
- On the other hand, male are more prone to death to COVID-19 as compared to female
15.7) Cases Over Province & Time Analysis ¶
- The province of Daegu, Gyeongsangbuk-do, Incheon and Seoul has the most amount of covid-19 infection cases among the 17 provinces; with Daegu accounting for more than half of the cases.
- The fatality count is relatively proportional to the infection count with the except of Seoul
- Bother Seoul and Gyeonggi-do has about 900 infected cases. However, Gyeonggi-do has about 22 fatalities and Seoul has about 7 fatalities.
15.8) Weather ¶
- The weather is about the same across the provinces.
- The temperature gradually increases from around 5 degree to 25 degree for the period of Jan 2020 to June 2020
- The weather is relatively the same across all provinces, it has little to do with the reported cases in the short term
15.9) Region ¶
- Number of nursing home vs Population Ratio
- We observed an interesting fact regarding the elderly population ratio and the number of nursing home in the city.
- The elderly population ratio and the number of nursing home has an inverse relationship
- Perhaps the absolute number of the elder people is smaller where elderly population ratio are high which explains why there is nursing home in places with higher elderly population ratio.
16) Preparing the data for modelling ¶
We will create a model which will predict whether a COVID-19 patient will survive given a certain set of conditions
- Sort city & province into different risk level according to number of confirmed cases (Low, Medium, High)
- Sort age into different age level according to age (kid, adult, elderly)
- Gender into categorical group of 0 & 1
- Number of treatment day
- Status of released, deceased into different category (We will ignore cases who are under treatment)
16.1) Get the necessary columns ¶
patientData = pd.read_csv('covid/patientinfo.csv')
patientModellingData = patientData[['sex','age','province','confirmed_date','released_date','deceased_date','state']]
## We removed isolated patient since it is not confirmed if they survived or not
patientModellingData = patientModellingData[patientModellingData['state'] != 'isolated']
nullList = ['sex','age','confirmed_date']
for item in nullList:
patientModellingData = patientModellingData[~patientModellingData[item].isnull()]
display(patientModellingData.head())
16.2) Calculate number of days of treatment before dropped date column ¶
cols = ['released_date', 'deceased_date', 'confirmed_date']
patientModellingData[cols] = patientModellingData[cols].apply(pd.to_datetime, errors='coerce', axis=1)
def calculate_number_of_treatment_days(row):
if row["released_date"] is not pd.NaT:
treatmentDays = pd.to_numeric((row['released_date'] - row['confirmed_date']).days)
return(treatmentDays)
elif row["deceased_date"] is not pd.NaT:
treatmentDays = pd.to_numeric((row['deceased_date'] - row['confirmed_date']).days)
return(treatmentDays)
else:
return None
patientModellingData['Treatment Days'] = patientModellingData.apply(calculate_number_of_treatment_days, axis=1)
patientModellingData = patientModellingData[~patientModellingData['Treatment Days'].isnull()]
patientModellingDataTreatment = patientModellingData[['sex','age','province','state','Treatment Days']]
display(patientModellingDataTreatment.head())
16.3) Convert state, gender and gender columns to categorical data ¶
genders = {"male": 0, "female": 1}
patientModellingDataTreatment['sex'] = patientModellingDataTreatment['sex'].map(genders)
display(patientModellingDataTreatment.head())
state = {"released": 0, "deceased": 1}
patientModellingDataTreatment['state'] = patientModellingDataTreatment['state'].map(state)
display(patientModellingDataTreatment.head())
age = {'0s':0, '10s':1, '20s':2, '30s':3, '40s':4, '50s':5, '60s':6, '70s':7, '80s':8, '90s':9}
patientModellingDataTreatment['age'] = patientModellingDataTreatment['age'].map(age)
display(patientModellingDataTreatment.head())
16.4) Get dummy for province ¶
provinceDummy = pd.get_dummies(patientModellingDataTreatment['province'])
provinceDummy
dataForModelling = patientModellingDataTreatment.join(provinceDummy)
dataForModelling = dataForModelling.drop('province',axis=1)
dataForModelling
17) Correlation Matrix ¶
plt.figure(figsize=(10,5))
sns.heatmap(dataForModelling.corr(), cmap="RdPu")
dataForModelling['age'] = pd.to_numeric(dataForModelling['age'])
dataForModellingForCleaning = dataForModelling.copy()
display(dataForModellingForCleaning.count())
print(np.any(np.isnan(dataForModellingForCleaning)))
print(np.all(np.isfinite(dataForModellingForCleaning)))
def clean_dataset(df):
assert isinstance(df, pd.DataFrame), "df needs to be a pd.DataFrame"
df.dropna(inplace=True)
indices_to_keep = ~df.isin([np.nan, np.inf, -np.inf]).any(1)
return df[indices_to_keep].astype(np.float64)
clean_dataset(dataForModellingForCleaning)
display(dataForModellingForCleaning.count())
print(np.any(np.isnan(dataForModellingForCleaning)))
print(np.all(np.isfinite(dataForModellingForCleaning)))
18) Building Machine Learning Models Part 1 ¶
x = dataForModellingForCleaning.drop("state", axis=1)
y = dataForModellingForCleaning["state"]
X_train, X_test, Y_train, Y_test = train_test_split(x, y, test_size=0.33, random_state=42)
18.1) Stochastic Gradient Descent (SGD): ¶
sgd = linear_model.SGDClassifier(max_iter=5, tol=None)
sgd.fit(X_train, Y_train)
Y_pred = sgd.predict(X_test)
sgd.score(X_train, Y_train)
acc_sgd = round(sgd.score(X_train, Y_train) * 100, 2)
18.2) Random Forest: ¶
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_prediction = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
18.3) Logistic Regression: ¶
logreg = LogisticRegression()
logreg.fit(X_train, Y_train)
Y_pred = logreg.predict(X_test)
acc_log = round(logreg.score(X_train, Y_train) * 100, 2)
18.4) Gaussian Naive Bayes: ¶
gaussian = GaussianNB()
gaussian.fit(X_train, Y_train)
Y_pred = gaussian.predict(X_test)
acc_gaussian = round(gaussian.score(X_train, Y_train) * 100, 2)
18.5) K Nearest Neighbor: ¶
knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train, Y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_train, Y_train) * 100, 2)
18.6) Perceptron: ¶
perceptron = Perceptron(max_iter=5)
perceptron.fit(X_train, Y_train)
Y_pred = perceptron.predict(X_test)
acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, 2)
18.7) Linear Support Vector Machine: ¶
linear_svc = LinearSVC()
linear_svc.fit(X_train, Y_train)
Y_pred = linear_svc.predict(X_test)
acc_linear_svc = round(linear_svc.score(X_train, Y_train) * 100, 2)
18.8) Decision Tree ¶
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
Y_pred = decision_tree.predict(X_test)
acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)
18.9) Getting the best model ¶
results = pd.DataFrame({
'Model': ['Support Vector Machines', 'KNN', 'Logistic Regression',
'Random Forest', 'Naive Bayes', 'Perceptron',
'Stochastic Gradient Decent',
'Decision Tree'],
'Score': [acc_linear_svc, acc_knn, acc_log,
acc_random_forest, acc_gaussian, acc_perceptron,
acc_sgd, acc_decision_tree]})
result_df = results.sort_values(by='Score', ascending=False)
result_df = result_df.set_index('Score')
result_df.head(9)
18.10) Decision Tree Diagram ¶
feature_cols = x.columns
dot_data = StringIO()
export_graphviz(decision_tree, out_file = dot_data,
feature_names = feature_cols,
filled = True, rounded = True,
special_characters = True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('covidTree.png')
Image(graph.create_png())
# Entropy 0 == no disorder // perfect knowledge, perfect classification
18.11) What is the most important feature ? ¶
importances = pd.DataFrame({'feature':X_train.columns,'importance':np.round(random_forest.feature_importances_,3)})
importances1 = importances.sort_values('importance',ascending=False).set_index('feature')
importances1.head(15)
barData = importances.reset_index()
fig = px.bar(barData, x='feature', y='importance')
fig.update_layout(hovermode='x')
fig.show()
Confusion Matrix with Precision & Recall & F-Score ¶
predictions = cross_val_predict(random_forest, X_train, Y_train, cv=3)
result1_train = confusion_matrix(Y_train, predictions)
display(result1_train)
p1_train = precision_score(Y_train, predictions)
r1_train = recall_score(Y_train, predictions)
f1_train = f1_score(Y_train, predictions)
print("Precision:", p1_train)
print("Recall:", r1_train)
print("F-Score:", f1_train)
predictions = cross_val_predict(random_forest, X_test, Y_test, cv=3)
result1_test = confusion_matrix(Y_test, predictions)
display(result1_test)
p1_test = precision_score(Y_test, predictions)
r1_test = recall_score(Y_test, predictions)
f1_test = f1_score(Y_test, predictions)
print("Precision:", p1_test)
print("Recall:", r1_test)
print("F-Score:", f1_test)
19) Building Machine Learning Models Part 2 ¶
Lets observe what happened if we drop the treatment days column Will the model be more accurate?
x2 = dataForModellingForCleaning.drop(["state","Treatment Days"], axis=1)
y2 = dataForModellingForCleaning["state"]
X_train, X_test, Y_train, Y_test = train_test_split(x2, y2, test_size=0.33, random_state=42)
19.1) Random Forest ¶
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_prediction = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
19.2) Decision Tree ¶
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
Y_pred = decision_tree.predict(X_test)
acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)
19.3) Getting the best model ¶
results = pd.DataFrame({
'Model': ['Random Forest','Decision Tree'],
'Score': [acc_random_forest, acc_decision_tree]})
result_df = results.sort_values(by='Score', ascending=False)
result_df = result_df.set_index('Score')
result_df.head(2)
19.4) Decision Tree Diagram ¶
feature_cols = x2.columns
dot_data = StringIO()
export_graphviz(decision_tree, out_file = dot_data,
feature_names = feature_cols,
filled = True, rounded = True,
special_characters = True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('covidTree2.png')
Image(graph.create_png())
19.5) Importance ¶
importances = pd.DataFrame({'feature':X_train.columns,'importance':np.round(random_forest.feature_importances_,3)})
importances2 = importances.sort_values('importance',ascending=False).set_index('feature')
importances2.head(15)
barData = importances.reset_index()
fig = px.bar(barData, x='feature', y='importance')
fig.update_layout(hovermode='x')
fig.show()
19.6) Confusion Matrix with Precision & Recall & F-Score ¶
predictions = cross_val_predict(random_forest, X_train, Y_train, cv=3)
result2_train = confusion_matrix(Y_train, predictions)
display(result2_train)
p2_train = precision_score(Y_train, predictions)
r2_train = recall_score(Y_train, predictions)
f2_train = f1_score(Y_train, predictions)
print("Precision:", p2_train)
print("Recall:", r2_train)
print("F-Score:", f2_train)
predictions = cross_val_predict(random_forest, X_test, Y_test, cv=3)
result2_test = confusion_matrix(Y_test, predictions)
display(result2_test)
p2_test = precision_score(Y_test, predictions)
r2_test = recall_score(Y_test, predictions)
f2_test = f1_score(Y_test, predictions)
print("Precision:", p2_test)
print("Recall:", r2_test)
print("F-Score:", f2_test)
20) Refine Dataset for Machine Learning ¶
Will the model's accuracy improve if we include patient who died without any treatment and the infected month?
patientData = pd.read_csv('covid/patientinfo.csv')
patientModellingData = patientData[['sex','age','province','confirmed_date','released_date','deceased_date','state']]
deadPatientModellingData = patientData[patientData['state'] == 'deceased']
totalDiedPatient = deadPatientModellingData.count()
display(totalDiedPatient)
display('***********')
pd.set_option('display.max_rows', deadPatientModellingData.shape[0]+1)
totalDiedPaitentWithoutTreatment = deadPatientModellingData[deadPatientModellingData['deceased_date'].isnull() == True].count()
display(totalDiedPaitentWithoutTreatment)
Assuming patient who died without any released_date or deceased_date are those died without any treatment
There are about 12 patient who died without any treatment
str(12/78 * 100) + '%'
This accounts for 15% of the total death
20.1) Preparing the data for modelling ¶
We will simply add another line of logic to return treatment days = 0
if the patient is deceased and both released and deceased date are empty
In addition, we will add in the month when the patient is confirmed to have covid cases
patientData = pd.read_csv('covid/patientinfo.csv')
patientModellingData = patientData[['sex','age','province','confirmed_date','released_date','deceased_date','state']]
## We removed isolated patient since it is not confirmed if they survived or not
patientModellingData = patientModellingData[patientModellingData['state'] != 'isolated']
nullList = ['sex','age','confirmed_date']
for item in nullList:
patientModellingData = patientModellingData[~patientModellingData[item].isnull()]
display(patientModellingData.head())
cols = ['released_date', 'deceased_date', 'confirmed_date']
patientModellingData[cols] = patientModellingData[cols].apply(pd.to_datetime, errors='coerce', axis=1)
def calculate_number_of_treatment_days(row):
if row["released_date"] is not pd.NaT:
treatmentDays = pd.to_numeric((row['released_date'] - row['confirmed_date']).days)
return(treatmentDays)
elif row["deceased_date"] is not pd.NaT:
treatmentDays = pd.to_numeric((row['deceased_date'] - row['confirmed_date']).days)
return(treatmentDays)
elif row["deceased_date"] is pd.NaT and row["released_date"] is pd.NaT:
if row["state"] == 'deceased' and row["state"] != 'released':
return 0
else:
return None
else:
return None
patientModellingData['Treatment Days'] = patientModellingData.apply(calculate_number_of_treatment_days, axis=1)
patientModellingData = patientModellingData[~patientModellingData['Treatment Days'].isnull()]
patientModellingDataTreatment = patientModellingData[['sex','age','confirmed_date','province','state','Treatment Days']]
patientModellingDataTreatment['confirmed_month'] = patientModellingDataTreatment['confirmed_date'].dt.month
patientModellingDataTreatment = patientModellingDataTreatment.drop('confirmed_date', axis=1)
display(patientModellingDataTreatment.head())
genders = {"male": 0, "female": 1}
patientModellingDataTreatment['sex'] = patientModellingDataTreatment['sex'].map(genders)
state = {"released": 0, "deceased": 1}
patientModellingDataTreatment['state'] = patientModellingDataTreatment['state'].map(state)
age = {'0s':0, '10s':1, '20s':2, '30s':3, '40s':4, '50s':5, '60s':6, '70s':7, '80s':8, '90s':9}
patientModellingDataTreatment['age'] = patientModellingDataTreatment['age'].map(age)
display(patientModellingDataTreatment.head())
dataForModelling = patientModellingDataTreatment.join(provinceDummy)
dataForModelling = dataForModelling.drop('province',axis=1)
dataForModelling
20.2) Building Machine Learning Models Part 3 ¶
clean_dataset(dataForModelling)
display(dataForModelling.count())
print(np.any(np.isnan(dataForModelling)))
print(np.all(np.isfinite(dataForModelling)))
x3 = dataForModelling.drop(["state"], axis=1)
y3 = dataForModelling["state"]
X_train, X_test, Y_train, Y_test = train_test_split(x3, y3, test_size=0.33, random_state=42)
## Random_forest
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_prediction = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
## Decision Tree
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
Y_pred = decision_tree.predict(X_test)
acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)
results = pd.DataFrame({
'Model': ['Random Forest','Decision Tree'],
'Score': [acc_random_forest, acc_decision_tree]})
result_df = results.sort_values(by='Score', ascending=False)
result_df = result_df.set_index('Score')
result_df.head(2)
20.3) Importances ¶
importances = pd.DataFrame({'feature':X_train.columns,'importance':np.round(random_forest.feature_importances_,3)})
importances3 = importances.sort_values('importance',ascending=False).set_index('feature')
importances3.head(15)
barData = importances.reset_index()
fig = px.bar(barData, x='feature', y='importance')
fig.update_layout(hovermode='x')
fig.show()
20.4) Confusion Matrix with Precision & Recall & F-Score ¶
predictions = cross_val_predict(random_forest, X_train, Y_train, cv=3)
result3_train = confusion_matrix(Y_train, predictions)
display(result3_train)
p3_train = precision_score(Y_train, predictions)
r3_train = recall_score(Y_train, predictions)
f3_train = f1_score(Y_train, predictions)
print("Precision:", p3_train)
print("Recall:", r3_train)
print("F-Score:",f3_train)
predictions = cross_val_predict(random_forest, X_test, Y_test, cv=3)
result3_test = confusion_matrix(Y_test, predictions)
display(result3_test)
p3_test = precision_score(Y_test, predictions)
r3_test = recall_score(Y_test, predictions)
f3_test = f1_score(Y_test, predictions)
print("Precision:", p3_test)
print("Recall:", r3_test)
print("F-Score:", f3_test)
20.5) Summary ¶
print('******************************')
print('Model without treatment day: ')
print('importance:', importances2.head(3))
display(result2_train)
display(result2_test)
print('Model with treatment day :')
print('importance:', importances1.head(3))
display(result1_train)
display(result1_test)
print('******************************')
print('Model with treatment day, those who died without treatment and infected month:')
print('importance:', importances3.head(3))
display(result3_train)
display(result3_test)
print('******************************')
print('Model without treatment day: ')
print("Train Data Precision:", p2_train)
print("Train Data Recall:", r2_train)
print("Train Data F-Score:", f2_train)
print("Test Data Precision:", p2_test)
print("Test Data Recall:", r2_test)
print("Test Data F-Score:", f2_test)
print('******************************')
print('Model with treatment day :')
print("Train Data Precision:", p1_train)
print("Train Data Recall:", r1_train)
print("Train Data F-Score:", f1_train)
print("Test Data Precision:", p1_test)
print("Test Data Recall:", r1_test)
print("Test Data F-Score:", f1_test)
print('******************************')
print('Model with treatment day, those who died without treatment and infected month:')
print("Train Data Precision:", p3_train)
print("Train Data Recall:", r3_train)
print("Train Data F-Score:", f3_train)
print("Test Data Precision:", p3_test)
print("Test Data Recall:", r3_test)
print("Test Data F-Score:", f3_test)
The Model with treatment day is better than the Model without treatment day even though it has a lower precision rate.
The number of survivor in COVID-19 is much higher than the number of deceased.
Hence, it is much harder to predict who will pass away from the infection.
The Model without treatment day is unable to predict whether a patient will pass away accurately.
The number of false negatives outweigh the number of true negatives.
On the other hand, the Model with treatment day is able to predict the deceased much accurately than the new model.
With that in mind, this also tell us that the number of days of treatment is vital.
The model accuracy improved after including the month which the patient is infected and those who died without treatment
21) Step to take to control the COVID-19 situation even better ¶
Generally, those who passed away from the infection had lesser days of treatment. However, is it right for us to conclude that lesser amount of treatment days, the higher the fatality rate? Are the risk of dying higher during first few days/weeks of treatment? Or is there something more to it?
21.1) Abraham Wald and the Missing Bullet Holes ¶
This situation is something similar to Abraham Wald and the Missing Bullet Holes. @penguinpress summed up the situation perfectly:
You don't want your planes to get shot down by enemy fighters, so you armor them. But armor makes the plane heavier, and heavier planes are less maneuverable and use more fuel. Armoring the planes too much is a problem; armoring the planes too little is a problem. Somewhere in between there's an optimum.
When American planes came back from engagements over Europe, they were covered in bullet holes. But the damage wasn't uniformly distributed across the aircraft. There were more bullet holes in the fuselage, not so many in the engines.
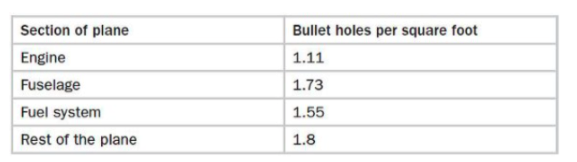
At first glance, it seems reasonable to focus the armor on the fuselage. However, the armor, said Wald, doesn't go where the bullet holes are. It goes where the bullet holes aren't: on the engines.
The missing bullet holes were on the missing planes. The reason planes were coming back with fewer hits to the engine is that planes that got hit in the engine weren't coming back.
If you go to the recovery room at the hospital, you'll see a lot more people with bullet holes in their legs than people with bullet holes in their chests. But that's not because people don't get shot in the chest; it's because the people who get shot in the chest don't recover.
The link to the excellent article written by @penguinpress is in the credit section below.
21.2) Survivorship Bias ¶
In this case, our model only consists of people who have passed away after they have gone through treatment. We have excluded people who have died even before they have the opportunity to go through treatment!
Even after we have excluded those who have not undergo treatment before they passed away, our model indicated that the number of treatment days is the strongest factor among gender, location and age. Treatment days has a whooping percentage of 60% in terms of importance next to age which has a importance of 20%.
21.3) Improving the situation ¶
The chances of survival increases as the number of treatment days increases. Hence, the faster detection rate, the earlier the treatment, the more days and opportunities to treat the infection, the better the chances of survival. The Korea government put a very strong emphasis on COVID-19 detection programme and hence they managed to contain the COVID-19 situation.
Various cities among the world were also in lockdown to prevent the rapid spread of COVID-19. The healthcare system will be overwhelmed if COVID-19 were to spread widely which will cause the death rate to escalate as more people will have lesser opportunity to undergo treatment.
The older the person, the higher the chances of infection and death. Hence it is not advisable for elderly people to roam around unless it is necessary.
In terms of locations, the majority of the cases came from Daegu and the sources of infection is from places such as church and clubs. The higher the amount of contact, the greater the chances of infection. It is advisable for the authority to close such areas until a vaccine for COVID-19 is found. During May to June, there is an increase in COVID-19 cases due to complacency.
https://www.aa.com.tr/en/asia-pacific/s-korea-sees-mass-covid-19-cases-linked-to-night-clubs/1838031
https://www.channelnewsasia.com/news/asia/south-korea-covid-19-church-backlash-13092284
22) References ¶
Soh, Z. (2020). 02a.bank-marketing.ipynb [Scholarly project]. Retrieved 2020.
Datartist. (2020, July 13). Data Science for COVID-19 (DS4C). Retrieved September 16, 2020, from https://www.kaggle.com/kimjihoo/coronavirusdataset
Press, P. (2016, July 14). Abraham Wald and the Missing Bullet Holes. Retrieved September 16, 2020, from https://medium.com/@penguinpress/an-excerpt-from-how-not-to-be-wrong-by-jordan-ellenberg-664e708cfc3d
Anand. (2019, March 11). Network Graph with AT&T data using Plotly. Retrieved September 16, 2020, from https://medium.com/@anand0427/network-graph-with-at-t-data-using-plotly-a319f9898a02
Donges, N. (2018, May 15). Predicting the Survival of Titanic Passengers. Retrieved September 16, 2020, from https://towardsdatascience.com/predicting-the-survival-of-titanic-passengers-30870ccc7e8
Rostami, D. (2020, March 22). Coronavirus Time Series Map Animation. Retrieved September 16, 2020, from https://datacrayon.com/posts/statistics/data-is-beautiful/coronavirus-time-series-map-animation/
23) Appendix ¶
Case.csv¶
case_id- The ID of the infection caseprovince- Special City / Metropolitan City / Province(-do)city- City(-si) / Country (-gun) / District (-gu)group- TRUE: group infection / FALSE: not groupinfection_case- the infection case (the name of group or other cases)confirmed- the accumulated number of the confirmedlatitude- the latitude of the group (WGS84)longitude- the longitude of the group (WGS84)
PatientInfo.csv¶
patient_id- the ID of the patientsex- the sex of the patientage- the age of the patientcountry- the country of the patientprovince- the province of the patientcity- the city of the patientinfection_case- the case of infectioninfected_by- the ID of who infected the patientcontact_number- the number of contacts with peoplesymptom_onset_date- the date of symptom onsetconfirmed_date- the date which the patient confirmed to have the viusreleased_date- the date which the patient is releaseddeceased_date- the date which the patient passed awaystate- the state of the patient: isolated, deceased, released
Policy.csv¶
policy_id- the ID of the policycountry- the country that implemented the policytype- the type of the policygov_policy- the policy of the governmentdetail- the detail of the policystart_date- the start date of the policyend_date- the end date of the policy
Region.csv¶
code- the code of the regionprovince- Special City / Metropolitan City / Province(-do)city- City(-si) / Country (-gun) / District (-gu)latitude- the latitude of the visit (WGS84)longitude- the longitude of the visit (WGS84)elementary_school_count- the number of elementary schoolskindergarten_count- the number of kindergartensuniversity_count- the number of universitiesacademy_ratio- the ratio of academieselderly_population_ratio- the ratio of the elderly populationelderly_alone_ratio- the ratio of the elderly who are alonenursing_home_count- the number of nursing home
SearchTrend.csv¶
date- YYYY-MM-DDcold- the search volume of 'cold' in Korean languageflu- the search volume of 'flu' in Korean languagepneumonia- the search volume of 'pneumonia' in Korean language
Time.csv¶
date- YYYY-MM-DDtime- Time (0 = AM 12:00 / 16 = PM 04:00)test- the accumulated number of testsnegative- the accumulated number of negative resultsconfirmed- the accumulated number of positive resultsreleased- the accumulated number of releasesdeceased- the accumulated number of deceases
TimeAge.csv¶
date- YYYY-MM-DDtime- Timeage- the age of patientsconfirmed- the accumulated number of the confirmeddeceased- the accumulated number of the deceased
TimeGender.csv¶
date- YYYY-MM-DDtime- Timesex- the gender of patientsconfirmed- the accumulated number of the confirmeddeceased- the accumulated number of the deceased
TimeProvince.csv¶
date- YYYY-MM-DDtime- Timeprovince- the province of South Koreaconfirmed- the accumulated number of the confirmed in the provincereleased- the accumulated number of the released in the provincedeceased- the accumulated number of the deceased in the province
Weather.csv¶
code- the code of the regionprovince- Special City / Metropolitan City / Province(-do)date- YYYY-MM-DDavg_temp- the average temperaturemin_temp- the lowest temperaturemax_temp- the highest temperatureprecipitation- the daily precipitationmax_wind_speed- the maximum wind speedmost_wind_direction- the most frequent wind directionavg_relative_humidity- the average relative humidity
24) Contribution Statements ¶
Yap Chee Ann (Victor)
- Build the overall structure of the project. Collaborate and compile project using parts from various teammates
- Data analysis, visualization and animation using pandas, plotly and networkx
- Implementation of machine learning model using sckit-learn to predict whether a patient will survive
- Deploy project to website for easy viewing
- Parts done: 1-5, 6.1-6.4, 7.1, 8.1-8.5, 9.1-9.2, 10-24
Yuan Yong Xi (Yannis)
- Conducted time series analysis including stationarity tests for confirmed cases and forecasting with ARIMA, ETS and LSTM models;
- Tested homogeneous mortality hypotheses across age, gender, and province groups with single-factor ANOVA;
- Validated distributional visualisations and machine learning mortality predictive models
- Parts done: 6.5-6.10, 7.2, 8.6, 9.3, 16, 20
Tan Zhi Yang
- Data analysis using pandas and matplotlib
- Gave good suggestion on how to data analysis and help team to keep a lookout for pitfall when doing data analysis
- Parts done: 3.1.2, 3.2.2, 4.1.2, 7.3, 7.4, 8.1-8.2, 9.4, 13.2
You Yu Quan
- Involved in discussion